

Luitzen Egbertus Jan Brouwer. Luitzen Egbertus Jan Brouwer ForMemRS[3] (Dutch: [ˈlœyt.sən ɛx.ˈbɛʁ.təs jɑn ˈbʁʌu.əʁ]; February 27, 1881 – December 2, 1966), usually cited as L.
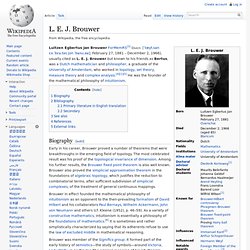
E. J. Brouwer but known to his friends as Bertus, was a Dutch mathematician and philosopher, a graduate of the University of Amsterdam, who worked in topology, set theory, measure theory and complex analysis.[4][1][5] He was the founder of the mathematical philosophy of intuitionism. Biography[edit] Early in his career, Brouwer proved a number of theorems that were breakthroughs in the emerging field of topology.
Brouwer was member of the Significs group. In 1905, at the age of 24, Brouwer expressed his philosophy of life in a short tract Life, Art and Mysticism described by Davis as "drenched in romantic pessimism" (Davis (2002), p. 94). "... He was combative for a young man. About his last years, Davis (2002) remarks: Bibliography[edit] Primary literature in English translation[edit] Secondary[edit] See also[edit] References[edit] Luitzen Egbertus Jan Brouwer. First published Wed Mar 26, 2003; substantive revision Fri May 6, 2011 Dutch mathematician and philosopher who lived from 1881 to 1966.
He is traditionally referred to as “L.E.J. Brouwer”, with full initials, but was called “Bertus” by his friends. In classical mathematics, he founded modern topology by establishing, for example, the topological invariance of dimension and the fixpoint theorem. He also gave the first correct definition of dimension. In philosophy, his brainchild is intuitionism, a revisionist foundation of mathematics. Biographie : Luitzen Egbertus Jan Brouwer. Théorème du point fixe de Brouwer. Un article de Wikipédia, l'encyclopédie libre. En 1886Henri Poincaré démontre un résultat équivalent au théorème du point fixe de Brouwer. L'énoncé exact est prouvé pour la dimension trois par Piers Bohl pour la première fois en 1904, puis par Jacques Hadamard dans le cas général en 1910.
Luitzen Brouwer propose une nouvelle démonstration en 1912. Point fixe, et théorèmes du point fixe. Qu'est-ce qu'un point fixe??? Soit E un ensemble et f : E->E une application. On dit que x. Théorème de l'invariance du domaine. Un article de Wikipédia, l'encyclopédie libre. En mathématiques, et plus précisément en topologie, le théorème de l'invariance du domaine est un résultat dû à L.E.J. Brouwer (1912)[1], concernant les applications continues entre sous-ensembles de Rn. Théorème de la boule chevelue. Un article de Wikipédia, l'encyclopédie libre. Si un champ de vecteurs tangents sur une sphère est symbolisé par des cheveux de longueur constante, le théorème de la boule chevelue stipule que la sphère contient au moins un épi.
La figure en contient deux, un sur chaque pôle. Sur un tore, la situation est différente. Logique intuitionniste. Un article de Wikipédia, l'encyclopédie libre. L'intuitionnisme est une position philosophique vis-à-vis des mathématiques proposée par le mathématicien hollandais Luitzen Egbertus Jan Brouwer comme une alternative à l'approche dite classique. Elle a été ensuite formalisée, sous le nom de logique intuitionniste, par ses élèves V. Glivenko et Arend Heyting. Kurt Gödel a montré que l'on pouvait représenter la logique classique dans la logique intuitionniste et ceci bien que l'ensemble des formules valides de la logique intuitionniste soit strictement inclus dans l'ensemble des formules valides de la logique classique.
Gerhard Gentzen en a formulé les règles de déduction dans le cadre de la déduction naturelle. Les travaux récents, notamment la correspondance de Curry-Howard, lui ont donné un statut central dans la logique et dans l'informatique, en faisant d'elle historiquement la première des logiques constructives. Approche informelle[modifier | modifier le code] et , tels que si ), puisque.