

Cours de Mathématiques en Mandala/Carte mentale: Suites Numériques. Présent depuis des millénaires au sein de plusieurs civilisations, le mandala, utilisé ici comme une "carte mentale", permet d'avoir une vue d'ensemble sur une notion, définition etc...
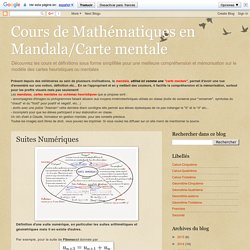
En se l'appropriant et en y mettant des couleurs, il facilite la compréhension et la mémorisation, surtout pour les profils visuels mais pas seulement! Les mandalas, cartes mentales ou schémas heuristiques que je propose sont :- accompagnés d'images ou pictogrammes faisant allusion aux moyens mnémotechniques utilisés en classe (boite de conserve pour "conserver", symboles du "chaud" et du "froid" pour positif et négatif, etc...)- écrits avec une police "Alamain" cette dernière étant curviligne elle permet aux élèves dyslexiques de ne pas mélanger le "b" et le "d" etc...- incomplets pour que les élèves participent à leur élaboration en classe.Un clin d'oeil à Claude, formateur en gestion mentale, pour ses conseils précieux.Toutes les images sont libres de droit, vous pouvez les imprimer.
Cartes heuristiques et Mathématiques (1) : un outil pour l'élève. Suite à une formation, voici le carnet de bord des réflexions d'une collègue de mathématiques en lycée à propos de la mise en oeuvre avec ses élèves d'un nouvel outil: les cartes heuristiques.
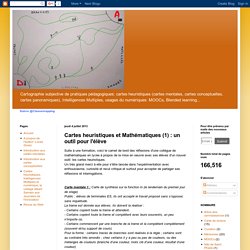
Un très grand merci à elle pour s'être lancée dans l'expérimentation avec enthousiasme, curiosité et recul critique et surtout pour accepter de partager ses réflexions et interrogations. Carte mentale 1 : Carte de synthèse sur la fonction ln (le lendemain du premier jour de stage)Public : élèves de terminales ES, ils ont accepté le travail proposé sans s’opposer, sans inquiétude.La trame est donnée aux élèves. Carte mentale 2: réaliser une carte bilan de cours sur les suites numériques.
(Aucune indication donnée)Je récupère les cartes après les vacances. Tous ont joué le jeu, les résultats sont très différents :- Certaines ont un contenu complètement erroné, les éléments qu’elles contiennent sont faux, sans lien logique… c’est effrayant…. ça ne sert à rien…. Maths, Info, etc. La méthode de datation des roches Rb/Sr est au programme de Sciences de la Vie et de la Terre en terminale S.
C'est une bonne occasion d'utiliser les connaissances du programme de mathématiques sur les fonctions exponentielle et logarithme. La méthode de datation Rb/Sr repose sur la présence d'atomes de rubidium et de strontium dans les roches. Rubidium Le rubidium est un métal alcalin. On s'intéresse à un isotope particulier du rubidium : le (^{87}Rb). La demi-vie du (^{87}Rb) est de (T=48,8) Ga, soit (48,8\times 10^9) années. De façon équivalente, on peut écrire : [^{87}Rb_{initial} = {}^{87}Rb_{actuel}\times e^{\lambda t}] Strontium Le strontium est un métal alcalino-terreux présent sous la forme de deux isotopes : Divisons maintenant l'équation ci-dessus par (^{86}Sr) : [\frac{^{87}Sr_{actuel}}{^{86}Sr} = \frac{{}^{87}Sr_{initial}}{^{86}Sr} + \frac{{}^{87}Rb_{actuel}}{^{86}Sr}(e^{\lambda t}-1)~~(1)] La méthode Le procédé de datation est donc le suivant : Justifications mathématiques.
Mathématiques - Les châteaux de cartes. Espace pédagogique > disciplines du second degré > mathématiques > enseignement > actions nationales > actions nationales 2007-2009 > Projets de scénarii (lycée) mis à jour le 09/04/2008 Une activité attractive pour donner du sens au concept difficile de suite numérique.
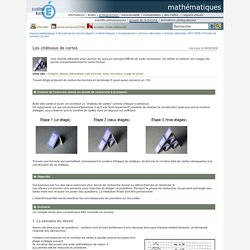
On utilise un tableur, les nuages de points et éventuellement le calcul formel. mots clés : initiative, tableur, automatiser, calcul formel, suite, récurence, nuage de points Travail dirigé et devoir de recherche donnés en terminale S (peut aussi convenir en 1S). Enoncé de l'exercice donné en devoir de recherche à la maison Avec des cartes à jouer, on construit un "château de cartes" comme indiqué ci-dessous.On supposera (ce qui est purement théorique !) Trouver une formule qui permettrait, connaissant le nombre d'étages du château, de donner le nombre total de cartes nécessaires à la construction de ce château.
Objectifs L'objectif essentiel est de réactiver les connaissances de première sur les suites. Scénario 1. 2. Suites numériques. Une même suite peut être fonctionnelle et être aussi définie par une relation de récurrence Dans la représentation graphique d'une suite définie par récurrence la droite d'équation y=x sert à ramener les termes ui sur l'axe des abscisses Pour étudier le sens de variation d'une suite, calculer les premiers termes ne suffit pas pour conclure sur le sens de variation de toute la suite Bien apprendre les formules concernant les suites arithmétiques et géométriques afin qu'elles soient directement disponilbles si besoin dans un problème Suites définies par une relation de récurrence 2) Représentation graphique D'une suite fonctionnelle.
The Fibonacci Sequence: Nature's Code.