

3D harmonic oscillator eigenfunctions - Curvature of the Mind. Yang–Mills existence and mass gap. In mathematical physics, the Yang–Mills existence and mass gap problem is an unsolved problem and one of the seven Millennium Prize Problems defined by the Clay Mathematics Institute which has offered a prize of US$1,000,000 to the one who solves it.
The problem is phrased as follows: Yang–Mills Existence and Mass Gap. Prove that for any compact simple gauge group G, a non-trivial quantum Yang–Mills theory exists on and has a mass gap Δ > 0. Existence includes establishing axiomatic properties at least as strong as those cited in Streater & Wightman (1964), Osterwalder & Schrader (1973) and Osterwalder & Schrader (1975). Quantum spacetime. In mathematical physics, the concept of quantum spacetime is a generalization of the usual concept of spacetime in which some variables that ordinarily commute are assumed not to commute and form a different Lie algebra.
The choice of that algebra still varies from theory to theory. As a result of this change some variables that are usually continuous may become discrete. Often only such discrete variables are called "quantized"; usage varies. Bloch sphere. Bloch sphere In quantum mechanics, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch.[1] Quantum mechanics is mathematically formulated in Hilbert space or projective Hilbert space.
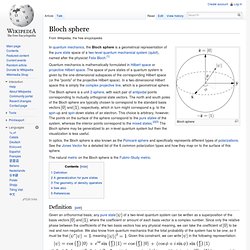
The space of pure states of a quantum system is given by the one-dimensional subspaces of the corresponding Hilbert space (or the "points" of the projective Hilbert space). In a two-dimensional Hilbert space this is simply the complex projective line, which is a geometrical sphere. The Bloch sphere is a unit 2-sphere, with each pair of antipodal points corresponding to mutually orthogonal state vectors. And. Schrödinger equation. In quantum mechanics, the Schrödinger equation is a partial differential equation that describes how the quantum state of some physical system changes with time.
It was formulated in late 1925, and published in 1926, by the Austrian physicist Erwin Schrödinger.[1] In classical mechanics, the equation of motion is Newton's second law, and equivalent formulations are the Euler–Lagrange equations and Hamilton's equations. Interpretations of quantum mechanics. An interpretation of quantum mechanics is a set of statements which attempt to explain how quantum mechanics informs our understanding of nature.
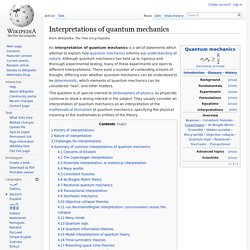
Although quantum mechanics has held up to rigorous and thorough experimental testing, many of these experiments are open to different interpretations. There exist a number of contending schools of thought, differing over whether quantum mechanics can be understood to be deterministic, which elements of quantum mechanics can be considered "real", and other matters. Matrix mechanics.
Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925.
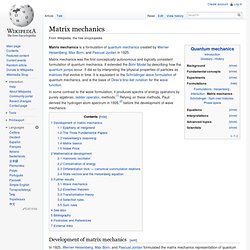
In some contrast to the wave formulation, it produces spectra of energy operators by purely algebraic, ladder operator, methods.[1] Relying on these methods, Pauli derived the hydrogen atom spectrum in 1926,[2] before the development of wave mechanics. Development of matrix mechanics[edit] In 1925, Werner Heisenberg, Max Born, and Pascual Jordan formulated the matrix mechanics representation of quantum mechanics. Epiphany at Helgoland[edit] In 1925 Werner Heisenberg was working in Göttingen on the problem of calculating the spectral lines of hydrogen. "It was about three o' clock at night when the final result of the calculation lay before me.
The Three Fundamental Papers[edit] After Heisenberg returned to Göttingen, he showed Wolfgang Pauli his calculations, commenting at one point:[4] In the paper, Heisenberg formulated quantum theory without sharp electron orbits. W. Lagrangian. The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system.
The Lagrangian is named after Italian-French mathematician and astronomer Joseph Louis Lagrange. Scalar field theory. In theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields.
A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field. The quanta of the quantized scalar field are spin-zero particles, and as such are bosons. The only fundamental scalar field that has been observed in nature is the Higgs field. However, scalar fields appear in the effective field theory descriptions of many physical phenomena.
An example is the pion, which is actually a "pseudoscalar", which means it is not invariant under parity transformations which invert the spatial directions, distinguishing it from a true scalar, which is parity-invariant. . , has a particularly simple form: it is diagonal, and here we use the + − − − sign convention. Chiral symmetry breaking. In particle physics, chiral symmetry breaking is an example of spontaneous symmetry breaking affecting the chiral symmetry of a gauge theory such as Quantum Chromodynamics, the quantum field theory of the strong interactions.
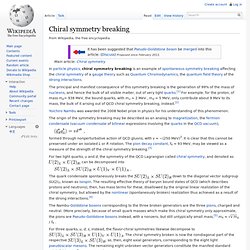
The principal and manifest consequence of this symmetry breaking is the generation of 99% of the mass of nucleons, and hence the bulk of all visible matter, out of very light quarks.[1] For example, for the proton, of mass mp= 938 MeV, the bound quarks, with mu ≈ 2 MeV , md ≈ 5 MeV, only contribute about 9 MeV to its mass, the bulk of it arising out of QCD chiral symmetry breaking, instead.[2] Yoichiro Nambu was awarded the 2008 Nobel prize in physics for his understanding of this phenomenon. The origin of the symmetry breaking may be described as an analog to magnetization, the fermion condensate (vacuum condensate of bilinear expressions involving the quarks in the QCD vacuum), formed through nonperturbative action of QCD gluons, with v ≈ −(250 MeV)3. .
Glueball. In particle physics, a glueball is a hypothetical composite particle.[1] It consists solely of gluon particles, without valence quarks.
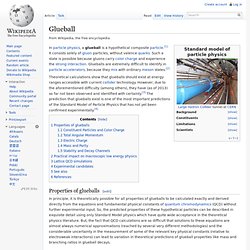
Such a state is possible because gluons carry color charge and experience the strong interaction. Glueballs are extremely difficult to identify in particle accelerators, because they mix with ordinary meson states.[2] Theoretical calculations show that glueballs should exist at energy ranges accessible with current collider technology. However, due to the aforementioned difficulty (among others), they have (as of 2013[update]) so far not been observed and identified with certainty.[3] The prediction that glueballs exist is one of the most important predictions of the Standard Model of Particle Physics that has not yet been confirmed experimentally.[4] Properties of glueballs[edit] Constituent Particles and Color Charge[edit] Total Angular Momentum[edit] Fundamental particles with J=0 or J=2 are easily distinguished from glueballs.
Electric Charge[edit] Wick rotation. In physics, Wick rotation, named after Gian-Carlo Wick, is a method of finding a solution to a mathematical problem in Minkowski space from a solution to a related problem in Euclidean space by means of a transformation that substitutes an imaginary-number variable for a real-number variable. This transformation is also used to find solutions to problems in quantum mechanics and other areas.
Overview[edit] Mass gap. In quantum field theory, the mass gap is the difference in energy between the vacuum and the next lowest energy state. The energy of the vacuum is zero by definition, and assuming that all energy states can be thought of as particles in plane-waves, the mass gap is the mass of the lightest particle. Since exact energy eigenstates are infinitely spread out and are therefore usually excluded from a formal mathematical description, a stronger definition is that the mass gap is the greatest lower bound of the energy of any state which is orthogonal to the vacuum. Mathematical definitions[edit] For a given real field.
Quantum gauge theory. Older approaches to quantization for Abelian models use the Gupta-Bleuler formalism with a "semi-Hilbert space" with an indefinite sesquilinear form. However, it is much more elegant to just work with the quotient space of vector field configurations by gauge transformations. An alternative approach using lattice approximations is covered in (Wick rotated) lattice gauge theory. Density matrix. Explicitly, suppose a quantum system may be found in state with probability p1, or it may be found in state with probability p2, or it may be found in state with probability p3, and so on. The density operator for this system is[1] By choosing a basis (which need not be orthogonal), one may resolve the density operator into the density matrix, whose elements are[1] For an operator (which describes an observable. Quantum geometry. In theoretical physics, quantum geometry is the set of new mathematical concepts generalizing the concepts of geometry whose understanding is necessary to describe the physical phenomena at very short distance scales (comparable to Planck length).
At these distances, quantum mechanics has a profound effect on physics. Quantum gravity[edit] In an alternative approach to quantum gravity called loop quantum gravity (LQG), the phrase "quantum geometry" usually refers to the formalism within LQG where the observables that capture the information about the geometry are now well defined operators on a Hilbert space. Efimov state.