


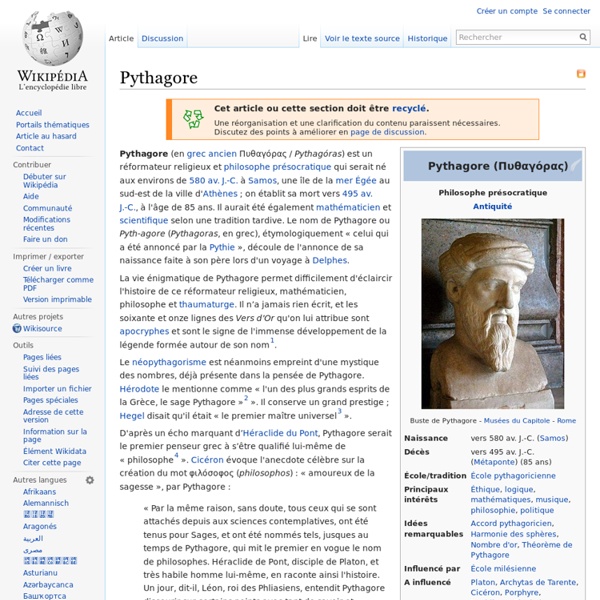
Pythagore «Pythagore est le créateur de la philosophie non seulement parce qu'il saisit le sens de la quête inachevée de l'homme, mais encore parce qu'il offre le terme de cette quête: la réalité éternelle qui explique à la fois le surgissement de l'existence relative et la perfection à laquelle elle est conviée. (...) Quel eût été le destin de la pensée grecque sans Pythagore? C'est de lui que dépendent Parménide, le créateur de l'ontologie, et Platon, le génie qui a donné son orientation définitive à cette pensée; et par le truchement de Platon, Aristote, l'orfèvre qui en a fixé la terminologie.» Pythagore a vécu en même temps que Lao-Tsé en Chine, Bouddha en Inde et Zarathoustra en Perse. Pythagore fut d'abord l'homme de la Méditerranée. Fut-il d'abord un maître spirituel, un savant ou un philosophe? Les disciples devaient d'abord faire un noviciat de cinq ans pendant lequel ils s'initiaient au silence. Voici comment Léon Brunschvicg évoque l'apport de Pythagore à l'humanité.
Héraion de Samos L'Héraion de Samos est un grand sanctuaire ionien, au sud de l'île de Samos, à 6 km au sud-ouest de l'ancienne cité, sur un terrain marécageux, près de la mer. Le site du sanctuaire, avec son unique colonne debout, est inscrit sur la liste du patrimoine mondial de l'Unesco, avec le Pythagoréion voisin, depuis 1992. Culte et mythologie[modifier | modifier le code] Naissance d'Héra[modifier | modifier le code] Le mythe fondateur du culte d'Héra à Samos est celui de sa naissance. Lors des grandes réunions samiennes annuelles, appelées Toneia (« les liens »), la statue de culte de la déesse était rituellement associée à des branches de lygos. Description du sanctuaire[modifier | modifier le code] Les premiers établissements[modifier | modifier le code] Les plus anciennes traces de construction du sanctuaire remontent au VIIIe siècle av. Le temple de Rhœcos[modifier | modifier le code] Le temple de Polycrate[modifier | modifier le code] L'autel d'Héra[modifier | modifier le code]
Théorème de Pythagore Un article de Wikipédia, l'encyclopédie libre. Cette page contient des caractères spéciaux. Si certains caractères de cet article s’affichent mal (carrés vides, points d’interrogation, etc.), consultez la page d’aide Unicode. Relation entre les longueurs des côtés dans un triangle rectangle. Le théorème de Pythagore est un théorème de géométrie euclidienne qui met en relation les longueurs des côtés dans un triangle rectangle : le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. Ce théorème permet notamment de calculer l’une de ces longueurs à partir des deux autres. Divers autres énoncés généralisent le théorème à des triangles quelconques, à des figures de plus grande dimension telles que les tétraèdres, ou en géométrie non euclidienne comme à la surface d’une sphère. Vocabulaire et énoncés Un triangle rectangle est un triangle admettant un angle droit (c’est-à-dire de mesure 90°, ou encore radians). Théorème est rectangle en , alors et
Heraion de Samos L'Héraion de Samos fut le premier des temples ioniques géants. Une des statues géantes (Kouros) du temple est conservée dans le Musée Archéologique. Une statue dite « Héra de Chéramyes » est exposée au Louvre. En 1992, il a été inscrit comme site du patrimoine mondial de l'UNESCO avec Pythagoreion situé à proximité. Il était situé à 6km au sud-ouest de l'ancienne cité de Samos . L'Heraion a traversé toute l'histoire artistique de la Grèce antique, avec d'importants remaniements et destructions. Celui-ci s'écroula près de dix ans après son édification, probablement à cause d'un tremblement de terre.
Théorème de Pythagore Cours de quatrième Le théorème de Pythagore est une propriété qui permet de calculer la longueur du troisième côté d'un triangle rectangle lorsqu'on connaît les longueurs des deux autres côtés. Pythagore était un mathématicien de la Grèce antique (en savoir plus). Théorème de Pythagore Vocabulaire Théorème de Pythagore Exemple Utiliser le théorème de Pythagore Pour utiliser le théorème de Pythagore, on doit connaître les longueurs de deux côtés d'un triangle rectangle. Méthode 1. Remarque Le théorème de Pythagore est particulièrement utile pour calculer des longueurs qu'on ne peut pas mesurer, comme des grandes distances sur la Terre ou dans l'espace (astronomie). Réciproque du théorème de Pythagore La réciproque du théorème de Pythagore est une propriété qui permet de dire si un triangle est rectangle ou non lorsqu'on connaît les longueurs de ses 3 côtés. Énoncé Méthode et exemple Bravo pour avoir lu ce cours jusqu'au bout. >>> Le cosinus >>> Le théorème de Pythagore sur cmath.fr Sur le web
Pythagoreion et Heraion de Samos Pythagoreion and Heraion of Samos Many civilizations have inhabited this small Aegean island, near Asia Minor, since the 3rd millennium B.C. The remains of Pythagoreion, an ancient fortified port with Greek and Roman monuments and a spectacular tunnel-aqueduct, as well as the Heraion, temple of the Samian Hera, can still be seen. Pythagoreion et Heraion de Samos Dans cette petite île de la mer Égée proche de l'Asie Mineure, plusieurs civilisations se sont succédé depuis le IIIe millénaire avant l'ère chrétienne. بيتاغوريون وهيرايون دي ساموس تعاقبت حضارات كثيرة منذ الألف الثالث قبل الحقبة المسيحية في هذه الجزيرة الصغيرة من بحر إيجة، وبقيت بصورة خاصة آثار بيتاغوريون المدينة المرفئية القديمة المحصّنة بنصبها اليونانية والرومانية، وقناة النفق الرائعة ، وهيرايون معبد الإلهة هيرا من ساموس. source: UNESCO/ERI 萨莫斯岛的毕达哥利翁及赫拉神殿 公元前3000年,这个靠近小亚细亚的爱琴海小岛上就有了文明。 Пифагорея и храм Геры на острове Самос Pitagoreion y Hereo de Samos サモス島のピュタゴリオンとヘラ神殿 source: NFUAJ Pythagorion en Heraion van Samos Source : unesco.nl
PYTHAGORE de Samos Détails Affichages : 132615 PYTHAGORE de Samos. Naissance: vers 569 av.J-C. à Samos, Ionie - Mort: vers 475 av.J.-C. à Crotone ? Sa vie. D'une génération plus jeune que Thalès, il aurait vécu dans la seconde moitié du 6ème siècle av. 1. Né à Samos (Grèce), Pythagore avait 18 ans lorsqu'il participa aux Jeux olympique et remporta toutes les compétitions de pugilat (sport de l' antiquité comparable à la boxe, mais dans lequel les combattants portaient au poing un gantelet garni de fer ou de plomb, la ceste). En Ionie toute proche, il passa quelques années auprès de Thalès et de son élève Anaximandre (v. 610 BC - v. 546 BC).Puis en Syrie, il séjourna avec les sages Vénitiens qui l' initièrent aux mystères de Byblos.Puis au mont Carmel, dans le Liban d' aujourd'hui.De là, il s' embarqua pour l' Égypte et y resta 20 années. Lorsque les Perses envahirent le pays, il se serait retrouvé prisonnier et emmené à Babylone. Pythagore a acquis ses connaissances mathématiques au cours de ses voyages.
Tunnel d'Eupalinos Le tunnel d'Eupalinos ou aqueduc d'Eupalinos (en grec : Ευπαλίνιον όρυγμα / Efpalínion órygma) est un aqueduc souterrain du VIe siècle av. J.-C., situé dans l'île de Samos, en Grèce. Selon les connaissances actuelles, c'est après le tunnel d'Ézéchias, la deuxième tentative réussie de forage d'un tunnel par les deux extrémités (en grec, αμφίστομον / amfístomon signifiant « ayant deux ouvertures »), et la première à faire appel à des plans méthodiques[1]. Avec ses 1 036 m de long, l'aqueduc souterrain d'Eupalinos de Mégare apparaît aujourd'hui comme l'un des chefs-d'œuvre antiques du génie civil, au même titre que le tunnel d'Ézéchias à Jérusalem. Histoire[modifier | modifier le code] L'île de Samos était gouvernée, au VIe siècle av. Sous les ordres de l'ingénieur Eupalinos de Mégare, deux équipes de travail creusèrent un aqueduc souterrain sous le mont Kastro afin d'alimenter en eau douce l'ancienne capitale de Samos (aujourd'hui Pythagorion). Description[modifier | modifier le code]
« La révolte de 1849-1850 dans la Principauté de Samos : Un aspect déviant du mouvement national grec », in M. Efthymiou (sous la direction de), La société grecque sous la domination ottomane. Economie, identité, structure sociale et conflits, Paris – Ath sujet historique — dans le cas qui nous occupe,le «peuple» ou la«communauté» de Samos—en groupes sociaux différents et analy-ser l’interaction entre ces groupes, au sein du système de pouvoirétabli, sont des conditions nécessaires pour la compréhension inter-prétative de la résultante de l’action sociale. Àcet égard, aprèsavoir brièvement présenté les événements, nous définirons lesacteurs principaux de l’insurrection, à savoir les différents groupessociaux de la société samienne de l’époque. Cette définition tiendracompte à la fois de critères objectifs et subjectifs — ou, plutôt,intersubjectifs. . NikolaosV. 2.Malheureusement, les actes de cette assemblée générale ont été égarés, ainsique ceux des assemblées de 1846 et de 1848. Sur Samos