Basic Trigonometric Graphs

Trigonometric Functions and Their Graphs: The Sine and Cosine (page 1 of 3) Sections: The sine and cosine, The tangent, The co-functions At first, trig ratios related only to right triangles. Then you learned how to find ratios for any angle, using all four quadrants. Then you learned about the unit circle, in which the value of the hypotenuse was always r = 1 so that sin(θ) = y and cos(θ) = x. In other words, you progressed from geometrical figures to a situation in which there was just one input (one angle measure, instead of three sides and an angle) leading to one output (the value of the trig ratio). Looking at the sine ratio in the four quadrants, we can take the input (the angle measure θ), "unwind" this from the unit circle, and put it on the horizontal axis of a standard graph in the x,y-plane. As you can see, the height of the red line, being the value of sin(θ) = y, is the same in each graph. The Sine Wave When you do your sine graphs, don't try to plot loads of points.

http://www.purplemath.com/modules/triggrph.htm

Radians to degrees How to convert degrees to radians or radians to degrees. Theory: What are 'radians' ? One radian is the angle of an arc created by wrapping the radius of a circle around its circumference. In this diagram, the radius has been wrapped around the circumference to create an angle of 1 radian. The pink lines show the radius being moved from the inside of the circle to the outside:

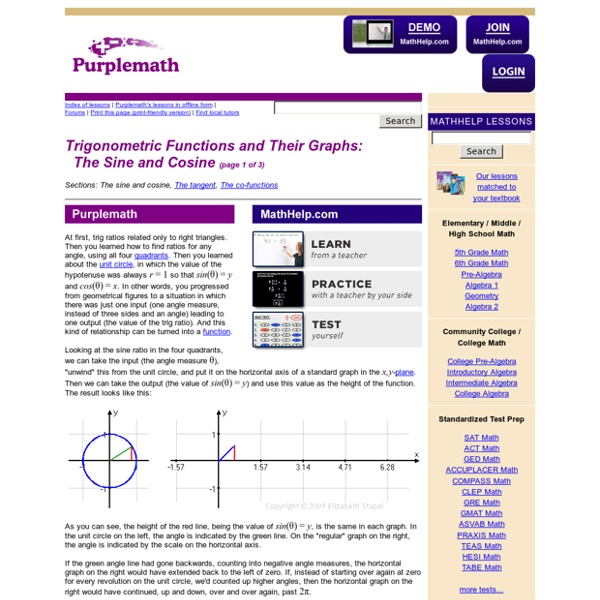
Graphing Trigonometric Functions Graphing Trigonometric Functions (page 1 of 3) Sections: Introduction, Examples with amplitude and vertical shift, Example with phase shift You've already learned the basic trig graphs. But just as you could make the basic quadratic x2, more complicated, such as –(x + 5)2 – 3, so also trig graphs can be made more complicated. We can transform and translate trig functions, just like you transformed and translated other functions in algebra.

Basic Trigonometric Graphs (tangent) Trigonometric Functions and Their Graphs: The Tangent (page 2 of 3) Sections: The sine and cosine, The tangent, The co-functions The next trig function is the tangent, but that's difficult to show on the unit circle. So let's take a closer look at the sine and cosines graphs, keeping in mind that tan(θ) = sin(θ)/cos(θ). The tangent will be zero wherever its numerator (the sine) is zero.

Graphing Sine The amplitude (maximum value) of y = sin x is 1. The period (the time it takes for one full cycle) of y = sinx is 2π. The midline of y = sinx is the x-axis. Review : Trig Functions The intent of this section is to remind you of some of the more important (from a Calculus standpoint…) topics from a trig class. One of the most important (but not the first) of these topics will be how to use the unit circle. We will actually leave the most important topic to the next section. First let’s start with the six trig functions and how they relate to each other. Recall as well that all the trig functions can be defined in terms of a right triangle. Solving Trigonometric Equations This section covers: Solving trig equations is just finding the solutions of equations like we did with linear, quadratic, and radical equations, but using trig functions instead. We will mainly use the Unit Circle to find the exact solutions if we can, and we’ll start out by finding the solutions from We can also solve these using a Graphing Calculator, as we’ll see below.

Graphs of trigonometric functions The Topics | Home Zeros of a function The graph of y = sin x The period of a function The graph of y = cos x Solving Trigonometric Equations Solving Trigonometric Equations (page 1 of 2) Solving trig equations use both the reference angles you've memorized and a lot of the algebra you've learned. Be prepared to need to think! Solve sin(x) + 2 = 3 for 0° < x < 360° Just as with linear equations, I'll first isolate the variable-containing term: sin(x) + 2 = 3 sin(x) = 1 Transformation of Trigonometric Graphs OML Search In these lessons, we will learn how Trigonometric Graphs can be transformed. the amplitude and vertical shift of Trigonometric Graphs the period and phase shift of Trigonometric Graphs

Transformations of the Sine and Cosine Graphs Transformations of the Sine and Cosine Graph – An Exploration By Sharon K. O’Kelley This is an exploration for Advanced Algebra or Precalculus teachers who have introduced their students to the basic sine and cosine graphs and now want their students to explore how changes to the equations affect the graphs. This is an introductory lesson whose purpose is to connect the language of Algebraic transformations to the more advanced topic of trignonometry. (A key follows the end of the exploration.)