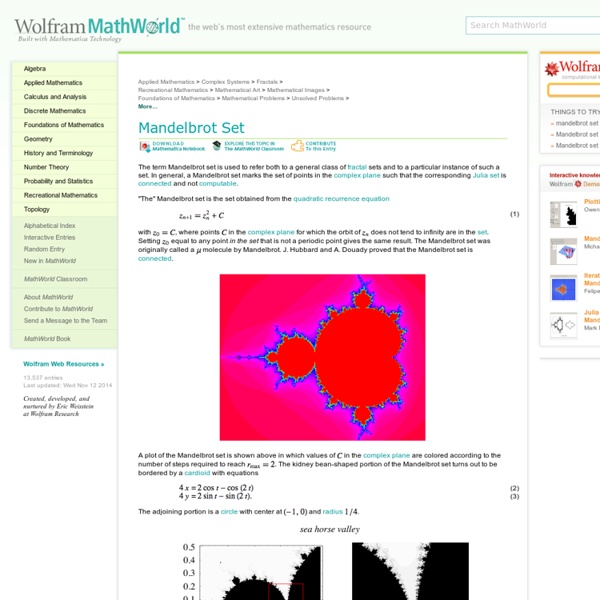
Mandelbrot Set

The term Mandelbrot set is used to refer both to a general class of fractal sets and to a particular instance of such a set. In general, a Mandelbrot set marks the set of points in the complex plane such that the corresponding Julia set is connected and not computable. "The" Mandelbrot set is the set obtained from the quadratic recurrence equation with , where points in the complex plane for which the orbit of does not tend to infinity are in the set. equal to any point in the set that is not a periodic point gives the same result. molecule by Mandelbrot. A plot of the Mandelbrot set is shown above in which values of in the complex plane are colored according to the number of steps required to reach . The adjoining portion is a circle with center at and radius The region of the Mandelbrot set centered around is sometimes known as the sea horse valley because the spiral shapes appearing in it resemble sea horse tails (Giffin, Munafo). Similarly, the portion of the Mandelbrot set centered around and

Box-and-Whisker Plots: Interquartile Ranges and Outliers Box-and-Whisker Plots: Interquartile Ranges and Outliers (page 3 of 3) Sections: Quartiles, boxes, and whiskers, Five-number summary, Interquartile ranges and outliers The "interquartile range", abbreviated "IQR", is just the width of the box in the box-and-whisker plot. That is, IQR = Q3 – Q1. The IQR is the length of the box in your box-and-whisker plot. (Why one and a half times the width of the box? Find the outliers, if any, for the following data set: To find out if there are any outliers, I first have to find the IQR. Outliers will be any points below Q1 – 1.5×IQR = 14.4 – 0.75 = 13.65 or above Q3 + 1.5×IQR = 14.9 + 0.75 = 15.65. Then the outliers are at 10.2, 15.9, and 16.4. The values for Q1 – 1.5×IQR and Q3 + 1.5×IQR are the "fences" that mark off the "reasonable" values from the outlier values. By the way, your book may refer to the value of "1.5×IQR" as being a "step". Find the outliers and extreme values, if any, for the following data set, and draw the box-and-whisker plot.

Lumosity Alcumus Alcumus offers students a customized learning experience, adjusting to student performance to deliver appropriate problems and lessons. Alcumus is specifically designed to provide high-performing students with a challenging curriculum appropriate to their abilities. Current features of Alcumus include: An intelligent learning system. As the student gets stronger, Alcumus automatically provides more challenging material, and conversely, if the student is having difficulty with a particular topic, Alcumus provides additional practice. Detailed progress reports. Students can track their performance in various subjects, and revisit problems and lessons at any time. Tools for teachers. Our Schola system allows teachers to monitor their students' progress and access Alcumus videos. Alcumus is currently free! You must have an account on the site in order to use Alcumus.