


Systemtheorie Die Systemtheorie ist sowohl eine allgemeine und eigenständige Disziplin als auch ein weitverzweigter und heterogener Rahmen für einen interdisziplinären Diskurs, der den Begriff System als Grundkonzept führt. Es gibt folglich sowohl eine allgemeine „Systemtheorie“ als auch eine Vielzahl unterschiedlicher, zum Teil widersprüchlicher und konkurrierender Systemdefinitionen und -begriffe. Es hat sich heute jedoch eine relativ stabile Reihe an Begriffen und Theoremen herausgebildet, auf die sich der systemtheoretische Diskurs bezieht. Geschichte[Bearbeiten] Der Begriff Allgemeine Systemtheorie geht auf den Biologen Ludwig von Bertalanffy zurück. Kulturgeschichtlich geht der Systembegriff bis auf Johann Heinrich Lambert zurück und wurde unter anderem von Johann Gottfried Herder übernommen und ausgearbeitet. Die moderne Systemtheorie beruht auf unabhängig voneinander entwickelten Ansätzen, die später synthetisiert und erweitert wurden: Der Begriff Systemtheorie bzw. Kybernetik[Bearbeiten]
Complex adaptive system They are complex in that they are dynamic networks of interactions, and their relationships are not aggregations of the individual static entities. They are adaptive in that the individual and collective behavior mutate and self-organize corresponding to the change-initiating micro-event or collection of events.[1][2] Overview[edit] The term complex adaptive systems, or complexity science, is often used to describe the loosely organized academic field that has grown up around the study of such systems. The fields of CAS and artificial life are closely related. The study of CAS focuses on complex, emergent and macroscopic properties of the system.[3][11][12] John H. General properties[edit] What distinguishes a CAS from a pure multi-agent system (MAS) is the focus on top-level properties and features like self-similarity, complexity, emergence and self-organization. Characteristics[edit] Some of the most important characteristics of complex systems are:[14] Robert Axelrod & Michael D.
Cellular automaton The concept was originally discovered in the 1940s by Stanislaw Ulam and John von Neumann while they were contemporaries at Los Alamos National Laboratory. While studied by some throughout the 1950s and 1960s, it was not until the 1970s and Conway's Game of Life, a two-dimensional cellular automaton, that interest in the subject expanded beyond academia. In the 1980s, Stephen Wolfram engaged in a systematic study of one-dimensional cellular automata, or what he calls elementary cellular automata; his research assistant Matthew Cook showed that one of these rules is Turing-complete. Wolfram published A New Kind of Science in 2002, claiming that cellular automata have applications in many fields of science. The primary classifications of cellular automata as outlined by Wolfram are numbered one to four. Overview[edit] The red cells are the von Neumann neighborhood for the blue cell, while the extended neighborhood includes the pink cells as well. A torus, a toroidal shape History[edit]
Self-organization Self-organization occurs in a variety of physical, chemical, biological, robotic, social and cognitive systems. Common examples include crystallization, the emergence of convection patterns in a liquid heated from below, chemical oscillators, swarming in groups of animals, and the way neural networks learn to recognize complex patterns. Overview[edit] The most robust and unambiguous examples[1] of self-organizing systems are from the physics of non-equilibrium processes. Self-organization is also relevant in chemistry, where it has often been taken as being synonymous with self-assembly. Self-organization usually relies on three basic ingredients:[3] Strong dynamical non-linearity, often though not necessarily involving positive and negative feedbackBalance of exploitation and explorationMultiple interactions Principles of self-organization[edit] History of the idea[edit] Sadi Carnot and Rudolf Clausius discovered the Second Law of Thermodynamics in the 19th century. Developing views[edit]
Encyclopedia of Complexity and Systems Science Assembles for the first time the concepts and tools for analyzing complex systems in a wide range of fields Reflects the real world by integrating complexity with the deterministic equations and concepts that define matter, energy, and the four forces identified in nature Benefits a broad audience: undergraduates, researchers and practitioners in mathematics and many related fields Encyclopedia of Complexity and Systems Science provides an authoritative single source for understanding and applying the concepts of complexity theory together with the tools and measures for analyzing complex systems in all fields of science and engineering. The science and tools of complexity and systems science include theories of self-organization, complex systems, synergetics, dynamical systems, turbulence, catastrophes, instabilities, nonlinearity, stochastic processes, chaos, neural networks, cellular automata, adaptive systems, and genetic algorithms. Content Level » Research Show all authors
Percolation threshold Percolation threshold is a mathematical term related to percolation theory , which is the formation of long-range connectivity in random systems. Below the threshold a giant connected component does not exist; while above it, there exists a giant component of the order of system size. In engineering and coffee making , percolation represents the flow of fluids through porous media, but in the mathematics and physics worlds it generally refers to simplified lattice models of random systems or networks (graphs), and the nature of the connectivity in them. [ edit ] Percolation models The most common percolation model is to take a regular lattice, like a square lattice, and make it into a random network by randomly "occupying" sites (vertices) or bonds (edges) with a statistically independent probability p . In the systems described so far, it has been assumed that the occupation of a site or bond is completely random—this is the so-called Bernoulli percolation. [ edit ] 2-Uniform Lattices
Agent-based model An agent-based model (ABM) is one of a class of computational models for simulating the actions and interactions of autonomous agents (both individual or collective entities such as organizations or groups) with a view to assessing their effects on the system as a whole. It combines elements of game theory, complex systems, emergence, computational sociology, multi-agent systems, and evolutionary programming. Monte Carlo Methods are used to introduce randomness. Agent-based models are a kind of microscale model [3] that simulate the simultaneous operations and interactions of multiple agents in an attempt to re-create and predict the appearance of complex phenomena. Most agent-based models are composed of: (1) numerous agents specified at various scales (typically referred to as agent-granularity); (2) decision-making heuristics; (3) learning rules or adaptive processes; (4) an interaction topology; and (5) a non-agent environment. History[edit] Early developments[edit] Theory[edit]
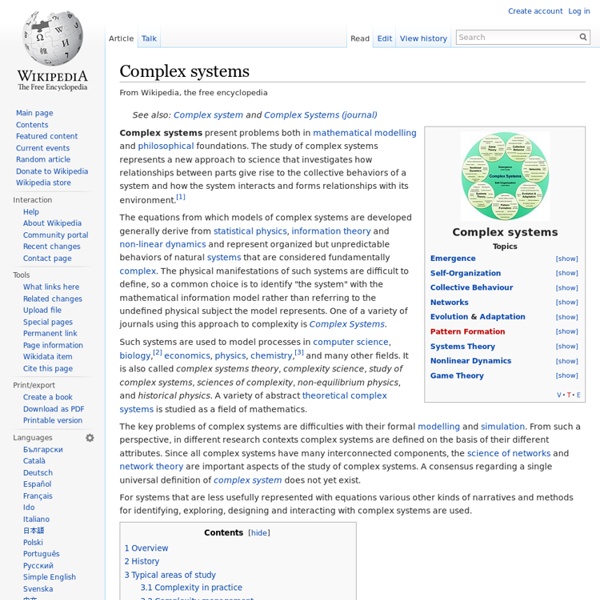
Emergence In philosophy, systems theory, science, and art, emergence is a process whereby larger entities, patterns, and regularities arise through interactions among smaller or simpler entities that themselves do not exhibit such properties. Emergence is central in theories of integrative levels and of complex systems. For instance, the phenomenon life as studied in biology is commonly perceived as an emergent property of interacting molecules as studied in chemistry, whose phenomena reflect interactions among elementary particles, modeled in particle physics, that at such higher mass—via substantial conglomeration—exhibit motion as modeled in gravitational physics. In philosophy, emergence typically refers to emergentism. In philosophy[edit] Main article: Emergentism In philosophy, emergence is often understood to be a claim about the etiology of a system's properties. Definitions[edit] This idea of emergence has been around since at least the time of Aristotle. Strong and weak emergence[edit]
Emergence : Complexity and Organization Articles - Find Articles at CBS MoneyWatch.com In Search of..... - TV.com www.tv.com/shows/in-search-of Narrarated by Leonard Nimoy, In search of was a 30 minute syndicated show that covered a wide range of paranormal topics. It pioneered a lot of the methodology that ... Search Engine - Download.com download.cnet.com/s/search-engine search engine free download - GSA Search Engine Ranker, Nomao - The personalized search engine, Zoom Search Engine, and many more programs Google Search - Download.com download.cnet.com/s/google-search google search free download - Google Search, Google Toolbar for Internet Explorer, Google Search, and many more programs Star Search - Episode Guide - TV.com www.tv.com/shows/star-search-2003/episodes Star Search episode guides on TV.com.
Complex adaptive system « Learning Change This book provides the first clear, comprehensive, and accessible account of complex adaptive social systems, by two of the field’s leading authorities. Such systems–whether political parties, stock markets, or ant colonies–present some of the most intriguing theoretical and practical challenges confronting the social sciences. Engagingly written, and balancing technical detail with intuitive explanations, Complex Adaptive Systems focuses on the key tools and ideas that have emerged in the field since the mid-1990s, as well as the techniques needed to investigate such systems. It provides a detailed introduction to concepts such as emergence, self-organized criticality, automata, networks, diversity, adaptation, and feedback. It also demonstrates how complex adaptive systems can be explored using methods ranging from mathematics to computational models of adaptive agents.
John H Miller Social Complex Systems Department Head and Professor of Economics and Social Science Office: PH 208D Phone: (412) 268-3229 Fax: (412) 268-6938 Education Ph.D.: University of Michigan, 1989 Research My research focuses on the complex adaptive behavior that emerges in social systems. To understand the behavior of complex adaptive systems, I have relied on the analysis of computational models composed of interacting artificial adaptive agents. Using artificial adaptive agent models, my colleagues and I have been able to analyze some central social phenomena. Complementing the above work, I have also pursued experimental and pure mathematical approaches to many of the above issues. Using the methods outlined above, previously inaccessible, yet fundamental, questions are now becoming amenable to analysis. Publications John H. John H. James Andreoni and John H. John H. Theodore Bergstrom and John H. John H. Ken Kollman, John H. John H. James Andreoni and John H. John Rust, John H. Ken Kollman, John H. John H.