CS 8803 - Game Theory and Computer Science. Spring 2008 - Theory
John von Neumann and the ENIAC Info Time: Tuesdays and Thursdays 9:35-10:55am Location: College of Computing, room 53 Instructor: Adam Tauman Kalai Grading: 50% Homework (Students may work alone or in groups of size at most 3. References: Some of the material for the class will be taken from the following books, but they are not required. Algorithmic Game Theory, edited by Nisan et al. Adam's Office hours: Thursday after class. TA: Atish Das Sarma, [Email: atish@cc.gatech.edu]. Lecture notes Assignments GTCS Assignment 1 Due 1/31/08. Syllabus John Nash Lloyd Shapley Efficiency Price of Anarchy Cooperative game theory Bargaining Nash, Kalai-Smorodinsky, and Egalitarian solutions Shapley value Core Bounded rationality Cryptography and game theory Funding is partly provided by NSF award SES-0734780.
Game theory
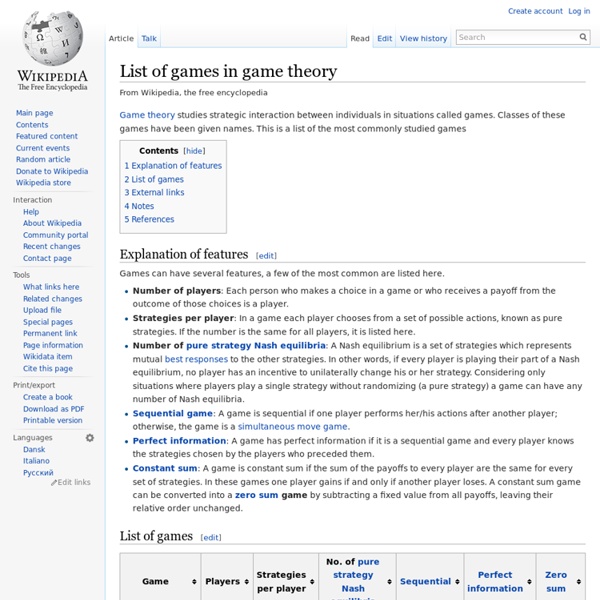
Game theory is the study of strategic decision making. Specifically, it is "the study of mathematical models of conflict and cooperation between intelligent rational decision-makers. Modern game theory began with the idea regarding the existence of mixed-strategy equilibria in two-person zero-sum games and its proof by John von Neumann. This theory was developed extensively in the 1950s by many scholars. Representation of games[edit] Most cooperative games are presented in the characteristic function form, while the extensive and the normal forms are used to define noncooperative games. Extensive form[edit] The game pictured consists of two players. The extensive form can also capture simultaneous-move games and games with imperfect information. Normal form[edit] When a game is presented in normal form, it is presumed that each player acts simultaneously or, at least, without knowing the actions of the other. Characteristic function form[edit] appears, it works against the fraction [edit]
David Levine's Economic and Game Theory Page
Game Theory
First published Sat Jan 25, 1997; substantive revision Wed May 5, 2010 Game theory is the study of the ways in which strategic interactions among economic agents produce outcomes with respect to the preferences (or utilities) of those agents, where the outcomes in question might have been intended by none of the agents. The meaning of this statement will not be clear to the non-expert until each of the italicized words and phrases has been explained and featured in some examples. 1. The mathematical theory of games was invented by John von Neumann and Oskar Morgenstern (1944). Despite the fact that game theory has been rendered mathematically and logically systematic only since 1944, game-theoretic insights can be found among commentators going back to ancient times. Long before game theory had come along to show analysts how to think about this sort of problem systematically, it had occurred to some actual military leaders and influenced their strategies. 2. 2.1 Utility
What is Game Theory?
Translations: Czech courtesy of Autip. Macedonian courtesy of Zoran Mitreski. Russian courtesy of Oleg Meister. German courtesy of Alexy Gnatuk. Romanian courtesy of Alexandra Seremina and Azoft. What economists call game theory psychologists call the theory of social situations, which is an accurate description of what game theory is about. In addition to game theory, economic theory has three other main branches: decision theory, general equilibrium theory and mechanism design theory. Decision theory can be viewed as a theory of one person games, or a game of a single player against nature. General equilibrium theory can be viewed as a specialized branch of game theory that deals with trade and production, and typically with a relatively large number of individual consumers and producers. Mechanism design theory differs from game theory in that game theory takes the rules of the game as given, while mechanism design theory asks about the consequences of different types of rules.
Game Theory .net - Resources for Learning and Teaching Strategy for Business and Life
All About Psychology- David Webb
CogLab: Wason Selection
Research has shown that people find it very difficult to decide what information is necessary in order to test the truth of an abstract logical-reasoning problem. The Wason Selection Task is often used to examine this issue. A typical experiment using the Wason Selection Task will present some rule, and ask subjects to see if the rule is being violated. Very few people can correctly pick the two cards to turn over to verify the rule. Consider another rule: If you borrow my car, you must fill up the gas tank. Which cards do you turn over to see if the rule is being followed? This lab is based on a series of experiments reported by Wason & Shapiro (1971).
Wason Selection Task
Each card has a number on one side, and a patch of color on the other. Which card(s) must be turned over to test the idea that if a card shows an even number on one face, then its opposite face is red? The Wason selection task (or four-card problem) is a logic puzzle devised by Peter Cathcart Wason in 1966.[1][2] It is one of the most famous tasks in the study of deductive reasoning.[3] An example of the puzzle is: You are shown a set of four cards placed on a table, each of which has a number on one side and a colored patch on the other side. A response that identifies a card that need not be inverted, or that fails to identify a card that needs to be inverted, is incorrect. The importance of the experiment is not in justifying one answer of the ambiguous problem, but in demonstrating the inconsistency of applying the logical rules by the people when the problem is set in two different contexts but with very similar connection between the facts. Solution[edit] Use of logic[edit]