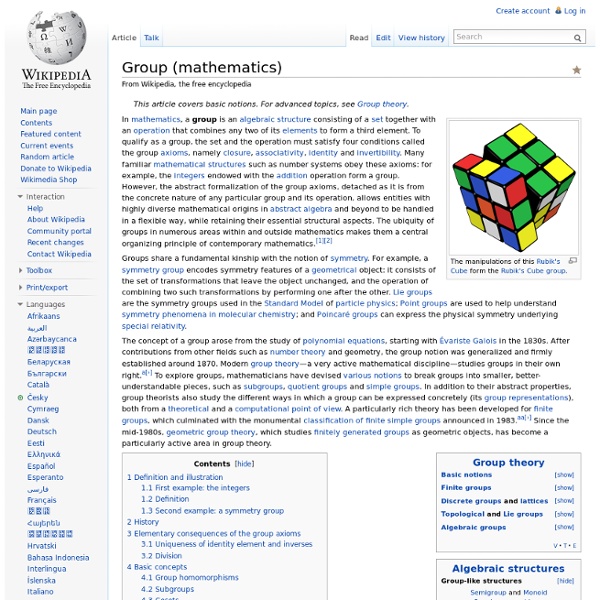
Group

Groups share a fundamental kinship with the notion of symmetry. For example, a symmetry group encodes symmetry features of a geometrical object: the group consists of the set of transformations that leave the object unchanged and the operation of combining two such transformations by performing one after the other. Lie groups are the symmetry groups used in the Standard Model of particle physics; Point groups are used to help understand symmetry phenomena in molecular chemistry; and Poincaré groups can express the physical symmetry underlying special relativity. One of the most familiar groups is the set of integers Z which consists of the numbers ..., −4, −3, −2, −1, 0, 1, 2, 3, 4, ...,[3] together with addition. The following properties of integer addition serve as a model for the abstract group axioms given in the definition below. The integers, together with the operation +, form a mathematical object belonging to a broad class sharing similar structural aspects. Closure Associativity

Subgroup A proper subgroup of a group G is a subgroup H which is a proper subset of G (i.e. H ≠ G). The trivial subgroup of any group is the subgroup {e} consisting of just the identity element. The same definitions apply more generally when G is an arbitrary semigroup, but this article will only deal with subgroups of groups. This article will write ab for a ∗ b, as is usual. Basic properties of subgroups[edit] G is the group , the integers mod 8 under addition. . Cosets and Lagrange's theorem[edit] If aH = Ha for every a in G, then H is said to be a normal subgroup. Example: Subgroups of Z8[edit] Let G be the cyclic group Z8 whose elements are and whose group operation is addition modulo eight. This group has two nontrivial subgroups: J={0,4} and H={0,2,4,6}, where J is also a subgroup of H. Example: Subgroups of S4 (the symmetric group on 4 elements)[edit] Every group has as many small subgroups as neutral elements on the main diagonal: The trivial group and two-element groups Z2. 12 elements[edit]

History of group theory Early 19th century[edit] The earliest study of groups as such probably goes back to the work of Lagrange in the late 18th century. However, this work was somewhat isolated, and 1846 publications of Cauchy and Galois are more commonly referred to as the beginning of group theory. The theory did not develop in a vacuum, and so 3 important threads in its pre-history are developed here. Development of permutation groups[edit] One foundational root of group theory was the quest of solutions of polynomial equations of degree higher than 4. An early source occurs in the problem of forming an equation of degree m having as its roots m of the roots of a given equation of degree n > m. A common foundation for the theory of equations on the basis of the group of permutations was found by mathematician Lagrange (1770, 1771), and on this was built the theory of substitutions. Ruffini (1799) attempted a proof of the impossibility of solving the quintic and higher equations. Felix Klein Sophus Lie

Symmetrization In mathematics, symmetrization is a process that converts any function in n variables to a symmetric function in n variables. Conversely, anti-symmetrization converts any function in n variables into an antisymmetric function. 2 variables[edit] Let be a set and an Abelian group. is termed a symmetric map if for all The symmetrization of a map is the map Conversely, the anti-symmetrization or skew-symmetrization of a map The sum of the symmetrization and the anti-symmetrization is Thus, away from 2, meaning if 2 is invertible, such as for the real numbers, one can divide by 2 and express every function as a sum of a symmetric function and an anti-symmetric function. The symmetrization of a symmetric map is simply its double, while the symmetrization of an alternating map is zero; similarly, the anti-symmetrization of a symmetric map is zero, while the anti-symmetrization of an anti-symmetric map is its double. Bilinear forms[edit] a function is skew-symmetric if and only if it is symmetric (as

ABSTRACT ALGEBRA: OnLine Study Guide, Table of Contents These online notes are for students who are working through our textbook Abstract Algebra. The notes are focused on solved problems, which are numbered consecutively, beginning with the exercises in the text. Our intention is to help students learn how to do proofs as well as computations. There are also some "lab" questions on groups, based on a Java applet Groups15 written by John Wavrik of UCSD. Some history Biographies (from the MacTutor History of Mathematics archives) Some help with logic and proofs Links to some algebra sites Chapter 1: INTEGERS Introduction 1.1 Divisors Problems Solutions 1.2 Primes Problems Solutions 1.3 Congruences Problems Solutions 1.4 Integers Modulo n Problems Solutions Review problems Solutions Chapter 2: FUNCTIONS Introduction 2.1 Functions Problems Solutions 2.2 Equivalence relations Problems Solutions 2.3 Permutations Problems Solutions Review problems Solutions Chapter 3: GROUPS Introduction 3.1 Definition of a Group Problems Solutions 3.2 Subgroups Problems Solutions