


Markov chains don’t converge I often hear people often say they’re using a burn-in period in MCMC to run a Markov chain until it converges. But Markov chains don’t converge, at least not the Markov chains that are useful in MCMC. These Markov chains wander around forever exploring the domain they’re sampling from. Not only that, Markov chains can’t remember how they got where they are. When someone says a Markov chain has converged, they may mean that the chain has entered a high-probability region. Burn-in may be ineffective. Why use burn-in? So why does it matter whether you start your Markov chain in a high-probability region? Samples from Markov chains don’t converge, but averages of functions applied to these samples may converge. It’s not just a matter of imprecise language when people say a Markov chain has converged.
Markov renewal process In probability and statistics a Markov renewal process is a random process that generalizes the notion of Markov jump processes. Other random processes like Markov chain, Poisson process, and renewal process can be derived as a special case of an MRP (Markov renewal process). Definition[edit] Consider a state space Consider a set of random variables , where are the jump times and are the associated states in the Markov chain (see Figure). . Relation to other stochastic processes[edit] If we define a new stochastic process for , then the process is called a semi-Markov process. See also[edit] References and Further Reading[edit]
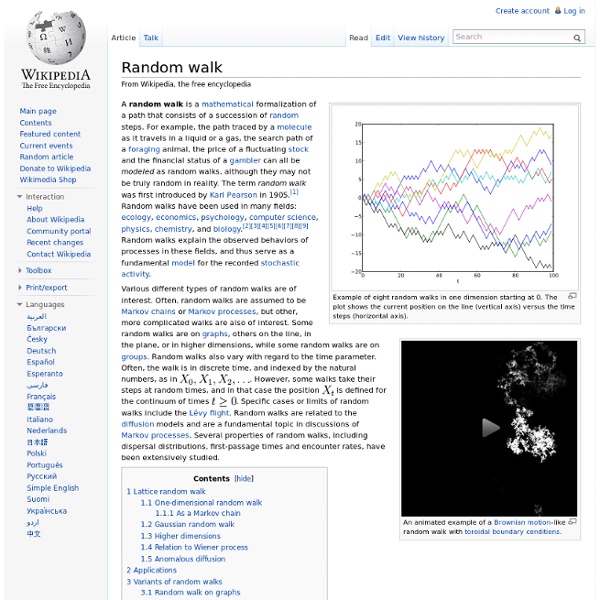
Markov chain A simple two-state Markov chain A Markov chain (discrete-time Markov chain or DTMC[1]), named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another on a state space. It is a random process usually characterized as memoryless: the next state depends only on the current state and not on the sequence of events that preceded it. This specific kind of "memorylessness" is called the Markov property. Markov chains have many applications as statistical models of real-world processes. Introduction[edit] A Markov chain is a stochastic process with the Markov property. In literature, different Markov processes are designated as "Markov chains". The changes of state of the system are called transitions. A discrete-time random process involves a system which is in a certain state at each step, with the state changing randomly between steps. Many other examples of Markov chains exist. Formal definition[edit] . . of states as input, where is defined, while and
Markov model Introduction[edit] The most common Markov models and their relationships are summarized in the following table: Markov chain[edit] The simplest Markov model is the Markov chain. It models the state of a system with a random variable that changes through time. Hidden Markov model[edit] A hidden Markov model is a Markov chain for which the state is only partially observable. Markov decision process[edit] A Markov decision process is a Markov chain in which state transitions depend on the current state and an action vector that is applied to the system. Partially observable Markov decision process[edit] A partially observable Markov decision process (POMDP) is a Markov decision process in which the state of the system is only partially observed. Markov random field[edit] A Markov random field (also called a Markov network) may be considered to be a generalization of a Markov chain in multiple dimensions. See also[edit] References[edit]
Markov process Markov process example Introduction[edit] A Markov process is a stochastic model that has the Markov property. Note that there is no definitive agreement in literature on the use of some of the terms that signify special cases of Markov processes. Markov processes arise in probability and statistics in one of two ways. Markov property[edit] The general case[edit] Let , for some (totally ordered) index set ; and let be a measurable space. adapted to the filtration is said to possess the Markov property with respect to the if, for each and each with s < t, A Markov process is a stochastic process which satisfies the Markov property with respect to its natural filtration. For discrete-time Markov chains[edit] In the case where is a discrete set with the discrete sigma algebra and , this can be reformulated as follows: Examples[edit] Gambling[edit] Suppose that you start with $10, and you wager $1 on an unending, fair, coin toss indefinitely, or until you lose all of your money. , then the sequence .
Interacting particle system In probability theory, an interacting particle system (IPS) is a stochastic process on some configuration space and a local state space, a compact metric space where is a finite set of sites and with for all . into configuration . on . of an IPS has the following form: Let be an observable in the domain of which is a subset of the real valued continuous function on the configuration space, then For example for the stochastic Ising model we have if for some and is the configuration equal to except it is flipped at site is a new parameter modeling the inverse temperature. Liggett, Thomas M. (1997).
Poisson process In probability theory, a Poisson process is a stochastic process that counts the number of events[note 1] and the time that these events occur in a given time interval. The time between each pair of consecutive events has an exponential distribution with parameter λ and each of these inter-arrival times is assumed to be independent of other inter-arrival times. The process is named after the French mathematician Siméon Denis Poisson and is a good model of radioactive decay,[1] telephone calls[2] and requests for a particular document on a web server,[3] among many other phenomena. The Poisson process is a continuous-time process; the sum of a Bernoulli process can be thought of as its discrete-time counterpart. A Poisson process is a pure-birth process, the simplest example of a birth-death process. Definition[edit] Consequences of this definition include: Other types of Poisson process are described below. Types[edit] Homogeneous[edit] Sample Path of a counting Poisson process N(t) , where .
Examples of Markov chains This page contains examples of Markov chains in action. Board games played with dice[edit] A game of snakes and ladders or any other game whose moves are determined entirely by dice is a Markov chain, indeed, an absorbing Markov chain. This is in contrast to card games such as blackjack, where the cards represent a 'memory' of the past moves. A center-biased random walk[edit] Consider a random walk on the number line where, at each step, the position (call it x) may change by +1 (to the right) or −1 (to the left) with probabilities: (where c is a constant greater than 0) For example if the constant, c, equals 1, the probabilities of a move to the left at positions x = −2,−1,0,1,2 are given by respectively. Since the probabilities depend only on the current position (value of x) and not on any prior positions, this biased random walk satisfies the definition of a Markov chain. A very simple weather model[edit] The above matrix as a graph. Predicting the weather[edit] or So Citation ranking[edit]
Poisson distribution Discrete probability distribution The Poisson distribution is named after French mathematician Siméon Denis Poisson (; French pronunciation: [pwasɔ̃]). It plays an important role for discrete-stable distributions. Under a Poisson distribution with the expectation of λ events in a given interval, the probability of k events in the same interval is:[2]: 60 For instance, consider a call center which receives, randomly, an average of λ = 3 calls per minute at all times of day. A classic example used to motivate the Poisson distribution is the number of radioactive decay events during a fixed observation period.[3] History In 1860, Simon Newcomb fitted the Poisson distribution to the number of stars found in a unit of space.[11] A further practical application was made by Ladislaus Bortkiewicz in 1898. Definitions Probability mass function A discrete random variable X is said to have a Poisson distribution, with parameter if it has a probability mass function given by:[2]: 60 where and:[14] Examples If