


List of common misconceptions From Wikipedia, the free encyclopedia Each entry on this list of common misconceptions is worded as a correction; the misconceptions themselves are implied rather than stated. These entries are concise summaries; the main subject articles can be consulted for more detail. A common misconception is a viewpoint or factoid that is often accepted as true but which is actually false. They generally arise from conventional wisdom (such as old wives' tales), stereotypes, superstitions, fallacies, a misunderstanding of science, or the popularization of pseudoscience. Some common misconceptions are also considered to be urban legends, and they are sometimes involved in moral panics. Arts and culture[edit] Business[edit] Federal legal tender laws in the United States do not require that private businesses, persons, or organizations accept cash for payment, though it must be treated as valid payment for debts when tendered to a creditor.[1] Food and cooking[edit] Food and drink history[edit] Music[edit]
Essential Math for Games Programmers As the quality of games has improved, more attention has been given to all aspects of a game to increase the feeling of reality during gameplay and distinguish it from its competitors. Mathematics provides much of the groundwork for this improvement in realism. And a large part of this improvement is due to the addition of physical simulation. This tutorial deepens the approach of the previous years' Essential Math for Games Programmers, by spending one day on general math topics, and one day focusing in on the topic of physical simulation. Topics for the various incarnations of this tutorial can be found below. Current Materials Slides The latest available versions of the slides for the math tutorials at GDC 2015 are as follows: See below for further materials from past years that may be useful. Past Materials Presentations for the math tutorials at GDC 2014 are as follows: Presentations for the math tutorials (the physics presentations are available here) at GDC 2013 are as follows:
10 Amazing Examples of Architecture Inspired by Mathematics The link between math and architecture goes back to ancient times, when the two disciplines were virtually indistinguishable. Pyramids and temples were some of the earliest examples of mathematical principles at work. Today, math continues to feature prominently in building design. We’re not just talking about mere measurements — though elements like that are integral to architecture. Mobius Strip Temple You probably made a Mobius Strip in grade school math class, so you should remember that the geometric form is unique in that there is no orientation. Wrap rage An example of wrap rage with a plastic light bulb package. Background[edit] Packaging sometimes must be made difficult to open. For example, regulations dictate that some over-the-counter drugs have tamper resistance to deter unauthorized opening prior to the intended customer and be in child-resistant packaging. Hard plastic blister packs also protect the products while they are being shipped.[2] In addition, using transparent plastic allows consumers to view products directly before purchasing them.[3] The term wrap rage itself came about as a result of media attention to the phenomenon. Frustration and injuries[edit] Consumers sometimes use potentially unsafe tools such as razor blades, boxcutters, snips and ice picks in their attempts to open packages.[2] In the Yours survey, 71% of respondents said they had been injured while trying to open food packaging. Solutions[edit] Packaging design[edit] Several methods of making packages easy to open have long been available. Opening[edit]
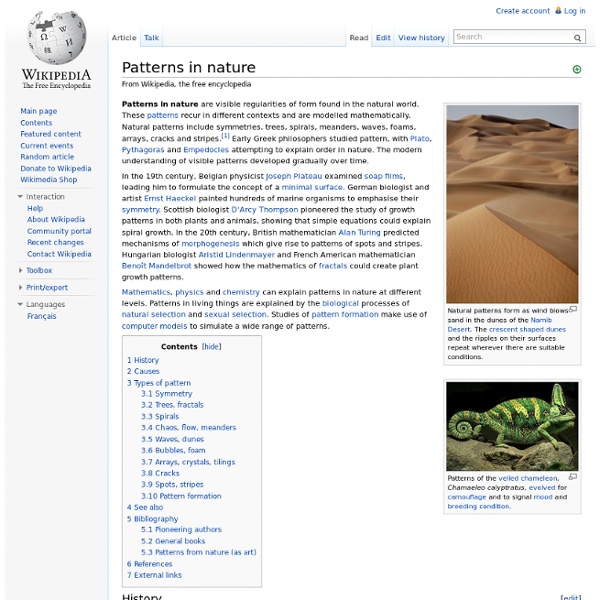
L-system L-system trees form realistic models of natural patterns Origins[edit] 'Weeds', generated using an L-system in 3D. As a biologist, Lindenmayer worked with yeast and filamentous fungi and studied the growth patterns of various types of algae, such as the blue/green bacteria Anabaena catenula. Originally the L-systems were devised to provide a formal description of the development of such simple multicellular organisms, and to illustrate the neighbourhood relationships between plant cells. Later on, this system was extended to describe higher plants and complex branching structures. L-system structure[edit] The recursive nature of the L-system rules leads to self-similarity and thereby, fractal-like forms are easy to describe with an L-system. L-system grammars are very similar to the semi-Thue grammar (see Chomsky hierarchy). G = (V, ω, P), where The rules of the L-system grammar are applied iteratively starting from the initial state. Examples of L-systems[edit] Example 1: Algae[edit] start : A
Mathematics and architecture Mathematics and architecture are related. Architects intentionally or accidentally use mathematical proportions to shape buildings. In ancient Greece, the golden ratio may have been used to lay out some buildings. In Renaissance architecture, symmetry and mathematical proportion were deliberately emphasized. In the twentieth century, styles such as modern architecture and Deconstructivism explored different geometries to achieve desired effects. Ancient times[edit] The Parthenon has been claimed to follow the proportions of the golden rectangle The ancient Egyptian pyramids at Giza have mathematical proportions, either by accident or by design. The Virupaksha temple at Hampi has a fractal-like structure where the parts resemble the whole. Ancient Greece[edit] In Greek architecture, the golden rectangle (also known as Phi, the golden section, golden ratio, or golden mean), served as a canon for planning architectural designs. Islamic architecture[edit] Other civilizations[edit] Renaissance[edit]
Dokkōdō The "Dokkōdō" [ (Japanese: 独行道?); "The Path of Aloneness", "The Way to Go Forth Alone", or "The Way of Walking Alone"] is a short work written by Miyamoto Musashi (宮本 武蔵) a week before he died in 1645. It consists of either nineteen or twenty-one precepts; precepts 4 and 20 are omitted from the former version. "Dokkodo" was largely composed on the occasion of Musashi giving away his possessions in preparation for death, and was dedicated to his favorite disciple, Terao Magonojō (to whom the earlier Go rin no sho [The Book of Five Rings] had also been dedicated), who took them to heart. "Dokkōdō" expresses a stringent, honest, and ascetic view of life. Precepts[edit] References[edit]
Guerrilla Tool Development I have a weak spot for cool game development tools. Not the IDE, or art or sound tools – I mean the level editors, AI construction tools – those that developers develop specifically for their games. Those that you know could help you multiply your content, and craft your game just a little bit better. Unfortunately, if you work on a small team, developing sophisticated tools like that is pretty much out of the question. That does not mean you have to hardcode everything, though. Here I will give you some ideas for getting tools for your game on a tight budget. Know your content creation tools inside out Before you even think about developing customised tools, it is extremely important to know your content-creation tools extremely well – even if you are not the content creator. As a programmer, you should focus on the following features: Automation Many art tools support some kind of batch processing. Data driven design This goes hand-in-hand with automation. Extensions Organisation Layers Tree