


Calculateur quantique Un article de Wikipédia, l'encyclopédie libre. Un calculateur quantique ou ordinateur[1] quantique repose sur des propriétés quantiques de la matière : superposition et intrication d'états quantiques. De petits calculateurs quantiques ont déjà été construits dès les années 1990 et la recherche progresse, bien que lentement, depuis. Ce domaine est soutenu financièrement par plusieurs organisations, entreprises ou gouvernements en raison de l'importance de l'enjeu : au moins un algorithme conçu pour utiliser un circuit quantique, l'algorithme de Shor, rendrait possible de nombreux calculs combinatoires[2] hors de portée d'un ordinateur classique en l'état actuel des connaissances. La possibilité de casser les méthodes cryptographiques classiques est souvent mise en avant. La difficulté actuelle majeure (depuis 2008) concerne la réalisation physique de l'élément de base de l'ordinateur quantique : le qubit. Intérêt des calculateurs quantiques[modifier | modifier le code]
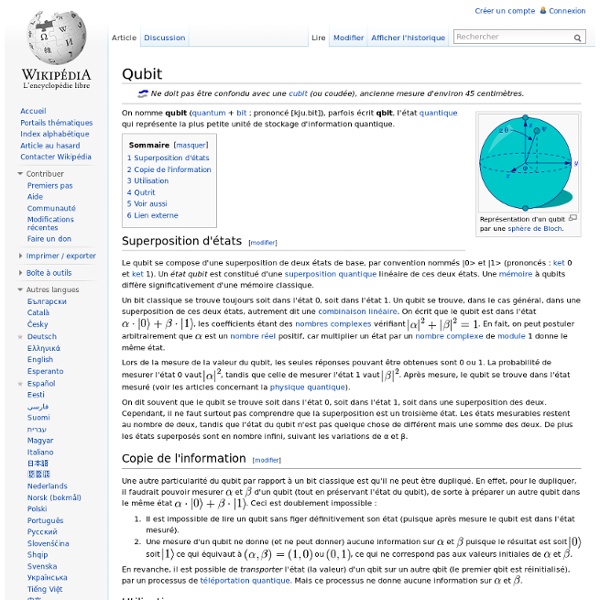
Qubit In quantum computing, a qubit/ˈkjuːbɪt/ or quantum bit is a unit of quantum information—the quantum analogue of the classical bit. A qubit is a two-state quantum-mechanical system, such as the polarization of a single photon: here the two states are vertical polarization and horizontal polarization. In a classical system, a bit would have to be in one state or the other, but quantum mechanics allows the qubit to be in a superposition of both states at the same time, a property which is fundamental to quantum computing. Bit versus qubit[edit] A bit is the basic unit of information. It is used to represent information by computers. A qubit has a few similarities to a classical bit, but is overall very different. Representation[edit] and (pronounced "ket 0" and "ket 1"). Qubit states[edit] Bloch sphere representation of a qubit. A pure qubit state is a linear superposition of the basis states. where and are probability amplitudes and can in general both be complex numbers. is . Bloch sphere[edit]
Algorithme de Shor Un article de Wikipédia, l'encyclopédie libre. En arithmétique modulaire et en informatique quantique, l’algorithme de Shor est un algorithme quantique pour factoriser un entier naturel N en temps O et en espace , nommé en l'honneur de Peter Shor. Beaucoup de cryptosystèmes à clé publique, tels que le RSA, deviendraient vulnérables si l'algorithme de Shor était un jour implémenté dans un calculateur quantique pratique. pour n'importe quel k, donc, les algorithmes classiques connus deviennent rapidement impraticables quand N augmente, à la différence de l'algorithme de Shor qui peut casser le RSA en temps polynomial. Comme tous les algorithmes pour calculateur quantique, l'algorithme de Shor est probabiliste : il donne la réponse correcte avec une haute probabilité et la probabilité d'échec peut être diminuée en répétant l'algorithme. L'algorithme de Shor fut utilisé en 2001 par un groupe d'IBM, qui factorisa 15 en 3 et 5, en utilisant un calculateur quantique de 7 qubits. I. II.
L'ordinateur quantique L’ordinateur quantique Une révolution technologique (I) Depuis l’invention du premier circuit intégré monolithique par Jack Kilby de Texas Instruments en 1958, l’intégration des composants électroniques n’a cessé d’être améliorée au point que nous parvenons aujourd’hui à faire fonctionner des centaines de milliers de composants sur une puce (chip) mesurant à peine 1 cm2, c’est la technologie ULSI (Ultra Large Scale Integration) qui détrône aujourd’hui le VLSI. A cette échelle les circuits mesurent une fraction de micron ! Mais à ce niveau de miniaturisation la difficulté de fabrication devient digne d’une mission impossible. Non seulement les effets quantiques deviennent apparents et peuvent générer des erreurs mais en cours de fonctionnement les composants dissipent beaucoup de chaleur, réduisant d’autant leur durée de vie. Pour tester ses performances en calcul pur, il fallait trouver un programme adapté à cette nouvelle architecture. Voici le compte-rendu de ces recherches. 1. 2.
L’ordinateur quantique se rapproche Je partage > Des chercheurs de l’université de nouvelle Galle du Sud, en Australie, ont mis au point un nouveau qubit en silicium. Ce bit quantique, brique fondamentale d’une (future ?) génération totalement nouvelle d’ordinateur, est particulièrement prometteur car il utilise les mêmes matériaux que l’électronique actuelle. Réutiliser les même processus industriels et le même matériel pourrait considérablement simplifier les prochaines étapes qu’il reste encore à franchir pour finaliser un ordinateur quantique complet. L’ordinateur quantique est un « vieux » rêve maintenant. Qu’est-ce qu’un ordinateur quantique d’ailleurs ? Un bit est un objet facile à concevoir, c’est un « zéro » ou un « un », matérialisé par le passage d’un courant dans un transistor. A la fois endormi et … endormi. Rappelons que le pauvre chat de ce savant est traditionnellement placé (en pensée, c’est une expérience hypothétique, heureusement) dans une boite pouvant être remplie d’un gaz mortel. source
Décohérence quantique Un article de Wikipédia, l'encyclopédie libre. La décohérence quantique est une théorie susceptible d'expliquer la transition entre les règles physiques quantiques et les règles physiques classiques telles que nous les connaissons, à un niveau macroscopique. Plus spécifiquement, cette théorie apporte une réponse, considérée comme étant la plus complète à ce jour, au paradoxe du chat de Schrödinger et au problème de la mesure quantique. La théorie de la décohérence a été introduite par Hans Dieter Zeh en 1970[1]. Elle a reçu ses premières confirmations expérimentales en 1996[2]. Introduction[modifier | modifier le code] Tous les objets décrits par la physique classique (projectile, planète, chat, etc.) étant composés, en dernière analyse, d'atomes et de particules, et ces derniers étant décrits entièrement par la physique quantique, il est logique de considérer que les règles de la physique classique peuvent se déduire de celles de la physique quantique. Durée[modifier | modifier le code] ou
L'ordinateur quantique (construction) Fabrication d’un ordinateur quantique (II) Depuis les travaux d'Einstein et consorts sur le paradoxe EPR en 1935 démontrant que l'intrication quantique était une réalité, de nombreuses expériences ont démontré qu'il était possible de contrôler l'intrication quantique entre deux photons, deux atomes, deux ions, dans des systèmes à semi-conducteurs tels que des spins d'ions, de noyaux et des points quantiques,,, des circuits supraconducteurs, ou encore dans des diamants colorés. En adaptant ces expériences aux contraintes de la théorie de l'information et donc aux ordinateurs, chacune de ces méthodes permet d'entrevoir la fabrication d'un calculateur voire d'un ordinateur quantique. Plusieurs technologies font appel à des molécules ou des atomes individuels ou encore à la polarisation d’une lumière laser comme support d’information. Une nouvelle fois le principal problème est la décohérence. 1. 2. 3. 4. 5. 6. 7. 1. Comment fonctionne un système à RMN ? 2. 3. 4. 5. En 2010, Gregory D. 6.
La téléportation quantique facilitée par un point quantique Le système de communication entre Alice et Bob (ELED est le point quantique intégré dans la DEL) Des scientifiques du centre de recherche européen de Toshiba et de l’université de Cambridge en Angleterre ont publié un papier important dans la revue Nature Photonics montrant qu’une boîte quantique (aussi appelée point quantique) est la solution la plus efficace pour assurer un système de communication reposant sur la téléportation quantique, selon Phys.org. Le point quantique était intégré au sein d’une DEL, une méthode de fabrication assez simple, qui permet de mieux contrôler les photons intriqués demandés par le système. Téléportation quantique La téléportation quantique est un protocole mis en avant en 1993 qui permet de transmettre l’état d’un qubit inconnu. Pour arriver à leurs fins, Alice et Bob vont partager deux qubits intriqués en plus du qubit inconnu d’Alice. L’apport du papier britannique
La molécule de chlorophylle serait un ordinateur quantique La molécule de chlorophylle serait un ordinateur quantique - 1 Photo Les membres du Fleming research group à l'origine de la découverte sur le mécanisme de la photosynthèse (à partir de la gauche) : Greg Engel , Tessa Calhoun, Tae-Kyu Ahn, Elizabeth Read et Yuan-Chung Cheng (Crédits : photo by Roy Kaltschmidt, Berkeley Lab Creative Services Office). Il est presque inutile de rappeler le rôle essentiel de la photosynthèse pour les différentes formes de vie sur Terre. Sous l'action du rayonnement solaire, les molécules de chlorophylle voient leurs niveaux électroniques excités et passer à un niveau d'énergie supérieur à ceux des molécules alentour. Jusqu'à présent, on pensait que les systèmes physiques exploraient de façon aléatoire, sur le principe d'une marche au hasard analogue au mouvement brownien, l'espace des états d'énergies impliqués. Gregory Engel et ses collègues pensent avoir percé le secret de cette efficacité ! A voir aussi sur Internet Sur le même sujet
L'ordinateur quantique (applications) L’ordinateur quantique Applications des ordinateurs quantiques (III) Admettons que notre ordinateur quantique soit fonctionnel. Un algorithme décrit de manière systématique les étapes de résolution d'un problème afin d'obtenir une solution, un résultat. Si nous lançons un calcul sur base d’un algorithme classique sur un ordinateur quantique, le processus ne tournera pas plus vite quoi qu’on fasse. Tout programmeur sait par exemple que si un calcul de multiplication est programmé sur un ordinateur supportant un encodage sur 8 bits, à vitesse CPU identique il n’ira pas plus vite s’il l’exécute sur une plate-forme 64 bits. C’est la même chose avec un ordinateur quantique. A présent, si notre programmeur utilise l’un de ces deux algorithmes sur un ordinateur quantique, il serait surpris par la vitesse d’exécution de son programme. A. Normalement, il faut N/2 recherches pour trouver un enregistrement dans une base de données contenant N entrées. B. C. La méthode à variables discrètes L’avenir
L’intrication quantique [Vidéo] Aujourd’hui une vidéo sur un phénomène bien mystérieux : l’intrication quantique. Comme toujours quand je traite de sujets de ce type en vidéo, j’aime bien apporter quelques compléments et précisions par écrit, qui je l’espère viendront éclairer ceux qui se posent encore des questions après le visionnage de la vidéo. Comme d’hab, c’est un peu un inventaire pas forcément très structuré de pensées diverses. L’expérience de déviation L’expérience de déviation dans un champ magnétique, on l’appelle l’expérience de Stern et Gerlach. Premièrement, j’ai dit dans la vidéo qu’on la faisait en balançant des atomes (et pas des électrons). Deuxième point caché dans la vidéo, pour qu’il y ait déviation il faut un gradient de champ magnétique, pas juste un champ uniforme ! C’est quoi exactement un état intriqué ? Dans la vidéo, j’ai choisi de présenter l’état intriqué le plus classique, celui de deux particules dont le spin total est nul Considérez par exemple l’état Les inégalités de Bell WordPress:
Comment l’informatique quantique pourrait révolutionner notre monde En poursuivant votre navigation sur ce site, vous acceptez nos CGU et l'utilisation de cookies afin de réaliser des statistiques d'audiences et vous proposer une navigation optimale, la possibilité de partager des contenus sur des réseaux sociaux ainsi que des services et offres adaptés à vos centres d'intérêts. Pour en savoir plus et paramétrer les cookies... Accueil GilbertKALLENBORN Journaliste Inscrivez-vous gratuitement à laNewsletter Actualités Calcul de molécules complexes, intelligence artificielle, problèmes d’optimisation… Les bénéfices de l’informatique quantique sont potentiellement énormes dans un grand nombre de domaines. Google, IBM, Intel, Microsoft… Depuis plusieurs mois, les géants de l'informatique multiplient les annonces pour montrer les efforts qu’ils entreprennent dans l’informatique quantique. Pour comprendre cet engouement général, il faut rappeler quelques principes du calcul quantique. Un parallélisme massif et naturel Trouver les molécules par un calcul exact
L'ordinateur quantique ThierryLombry Informaticien Depuis l'invention du premier circuit intégré monolithique par Jack Kilby de Texas Instruments en 1958, l'intégration des composants électroniques n'a cessé d'être améliorée au point que nous parvenons aujourd'hui à faire fonctionner des centaines de milliers de composants sur une puce (chip) mesurant à peine 1 cm2, c'est la technologie ULSI (Ultra Large Scale Integration) qui détrône aujourd'hui le VLSI. A cette échelle les circuits mesurent une fraction de micron ! Le coeur de l'ordinateur : le microprocesseur Mais à cette échelle la difficulté de fabrication devient digne d'une mission impossible. Représentation artistique des fameux bits quantiques ou qubits. © U.Melbourne/Marc Coe.
Quantum Computing Playground A classic computer processes bits, which at any given time can be in one of two states: 0 or 1. Quantum computers use qubits, which can exist in any superposition of states 0 and 1, and are represented by a complex number. When N qubits are in superposition, a combination of 2^N states is created. The most basic operations performed on qubits are defined by quantum gates, similar to logical gates used in classic computers. As of today the only company selling quantum computers is D-Wave, but unfortunately their architecture does not perform arbitrary quantum gate operations on sequences of qubits (which is what Quantum Computing Playground simulates at this time).