Harmonic series (music)
Harmonic series of a string with terms written as reciprocals (2/1 written as 1/2). A harmonic series is the sequence of all multiples of a base frequency. Any complex tone "can be described as a combination of many simple periodic waves (i.e., sine waves) or partials, each with its own frequency of vibration, amplitude, and phase."[1] (Fourier analysis) A partial is any of the sine waves by which a complex tone is described. A harmonic (or a harmonic partial) is any of a set of partials that are whole number multiples of a common fundamental frequency.[2] This set includes the fundamental, which is a whole number multiple of itself (1 times itself). Typical pitched instruments are designed to have partials that are close to being harmonics, with very low inharmonicity; therefore, in music theory, and in instrument tuning, it is convenient to speak of the partials in those instruments' sounds as harmonics, even if they have some inharmonicity. An overtone is any partial except the lowest.
Pythagorean tuning
The syntonic tuning continuum, showing Pythagorean tuning at 702 cents.[1] Diatonic scale on C Play 12-tone equal tempered and Play just intonation. Pythagorean (tonic) major chord on C Play (compare Play equal tempered and Play just). Comparison of equal-tempered (black) and Pythagorean (green) intervals showing the relationship between frequency ratio and the intervals' values, in cents. The system had been mainly attributed to Pythagoras (sixth century BC) by modern authors of music theory, while Ptolemy, and later Boethius, ascribed the division of the tetrachord by only two intervals, called "semitonium", "tonus", "tonus" in Latin (256:243 x 9:8 x 9:8), to Eratosthenes. Method[edit] Pythagorean tuning is based on a stack of intervals called perfect fifths, each tuned in the ratio 3:2, the next simplest ratio after 2:1. This succession of eleven 3:2 intervals spans across a wide range of frequency (on a piano keyboard, it encompasses 77 keys). Size of intervals[edit] (e.g. between E♭ and E)
How To Read Sheet Music – Music Education 101
Learning to read sheet music can seem daunting to some people, especially those with no prior musical background. Sheet music contains its own little language documented on paper. The key is to find a way to crack the code, read music, and be able to play or sing on the pitch of each note. If you want to learn how to read music, then you have come to the right place. If you want to learn more -- and in one night, no less -- here's a recommendation: Learn to Read Music In One Evening. The structure of sheet music. Other common time signatures are 2/2 time (cut time), 2/4 time, 3/4 time, and 6/8 time. Notes, notes, and more notes. The left hand of a pianist is used to play the notes on the bass clef of piano sheet music. Learn from a professional - Take music lessons. There are many different places you can take music lessons. To find a musical professional in your area you can check out: Study on your own. Learning how to read sheet music should be fun.
Schillinger System
The Schillinger System of Musical Composition, named after Joseph Schillinger, is a method of musical composition based on mathematical processes. It comprises theories of rhythm, harmony, melody, counterpoint, form, and semantics (emotional meaning, as in movie music). It offers a systematic and non-genre specific approach to music analysis and composition, a descriptive rather than prescriptive grammar of music. The Schillinger System might have served as a road map for many later developments in music theory and composition. Instead, it languished in relative obscurity. Schillinger's career[edit] Schillinger was a professor at The New School in New York City and taught such celebrated musicians as George Gershwin, Glenn Miller, Benny Goodman, and a host of Hollywood and Broadway composers. In New York, Schillinger flourished, becoming famous as the advisor to many of America's leading popular musicians and concert music composers. After Schillinger[edit] Beyond style[edit] Students[edit]
Interactive Circle of Fifths User's Guide
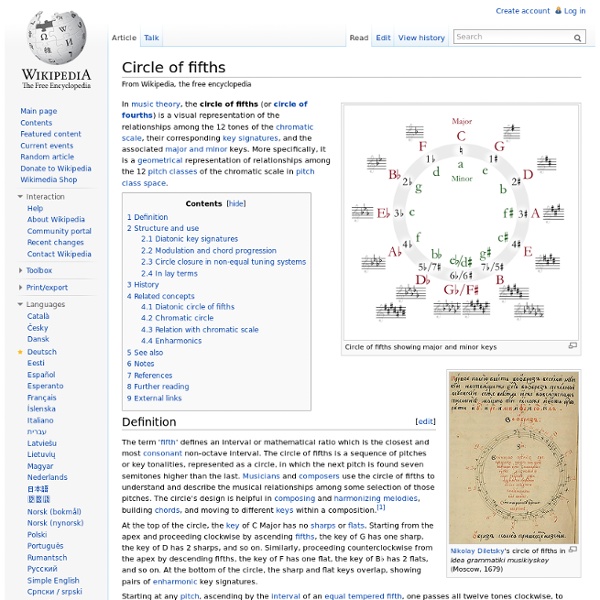
The Interactive Circle of Fifths ("the Circle" for short) is a tool designed to help musicians to: figure out the key of a piece of music easily transpose music to a different key compose new music understand key signatures, scales, and modes The concept of the circle of fifths is not a new one (see this Wikipedia article for more information), but there is more to this simple, yet profound structure than the traditional diagram can easily convey. The Interactive Circle of Fifths goes beyond the limitations of a static diagram without sacrificing clarity and simplicity. This User's Guide will help you get the most out of the Circle, while introducing some basic music theory concepts. Using the Circle Offline: You can easily download a copy of the Circle to use when you don't have an Internet connection: If you use Internet Explorer or Opera: Use the Save As... command in the browser's File menu, and save as type "Web Archive, single file (*.mht)". (seven sharps) through C (seven flats). .
Why the circle of fourths is so important when learning major scales | Hear and Play Music Learning Center
Playing your major scales should be a part of your daily practice regimen. However, practicing them in a “circle of fourths” or “circle of fifths” pattern is even better. Let’s focus more on circle of fourths. If you type “circle of fourths” or “circle of fifths” in google, you can actually find a host of other examples. Notice that the keys go from: C >>> F >>> Bb >>> Eb and so forth. If this were a clock, C would be at 12 o’ clock. This is the optimal way to play your scales. Then play your F major scale all the way through (F G A Bb C D E F). Why the circle? Because music also happens to move in this same pattern (way beyond the scope of this article but I’ll touch on it a little bit). But here’s another reason to use the circle. Because it lets you know how related the major keys are to each other. If one just looked at a piano, they’d assume that C and Db, for example, were related because of how close they appear to each other on the piano. The reality is that C and F are more related.
Untitled Document
Mathematics, astronomy, geometry, geography, art, music and religion were all integrated in ancient times. Numerous surviving examples suggest that ancient Egyptian art was based on a strict canon that was followed for over 3,000 years. According to Plato, this was also true of ancient Egyptian music. Tone is based on the frequency of sound waves. The next higher octave may be calculated by doubling the frequency of each note and the next lower octave may be calculated by halving the frequency of each note. A string tuned to a base frequency of 440 waves per second (440 Hz) will also produce higher tones known as partials or harmonics. When the same note is played by two different instruments at the same time, the frequency of both notes is the same, so every wave of both notes aligns, resulting in optimal consonance. What Pythagoras described as perfect fifths and perfect fourths are notes with low integer ratios in relation to the base note, also resulting in consonant sound.
Indian Classical Music mapped to Western Music