


Vous avez du mal avec les multiplications ? Essayez cette méthode étonnante Si vous n'êtes pas très doué pour poser et résoudre les multiplications, peut-être serez vous plus à l'aise avec la méthode japonaise. Elle consiste à dessiner des lignes et compter des points pour trouver le résultat d'une multiplication. Explications en vidéo. Pas facile de multiplier des nombres à deux chiffres de tête ! Il suffit de matérialiser chaque chiffre par une ligne. En regroupant les lignes et en comptant le nombre d’intersections dans chaque groupe, on trouve une combinaison de chiffres qui donne le résultat. Appelée ‘méthode japonaise’, cette technique peut être utile pour des multiplications relativement simples.
Récréomath Site de mathématiques récréatives Arbre de vie Un article de Wikipédia, l'encyclopédie libre. Arbre de vie entouré de deux panthères tenant une corne d'abondance (haut-relief sculpté sur le portique sud de la Maria Saal, District de Klagenfurt, Carintie, Autriche) Les arbres de vie gravés, peints, brodés, imprimés ou sculptés existent depuis le début de l'Histoire. Ils semblent symboliser la force de la vie et ses origines, l'importance des racines et le développement de la Vie. Dans la Bible[modifier | modifier le code] À partir du Ve siècle, avec Augustin d'Hippone, les chrétiens ont développé en fonction de ces passages de la Genèse et d'épîtres de saint Paul diverses théologies dites du « péché originel ». Cet arbre est aussi mentionné plusieurs fois dans l'Apocalypse (Ap 2, 7[4] ; Ap 22, 14 ; Ap 22, 19[5]). Dans la Kabbale[modifier | modifier le code] Dans le livre de Mormon[modifier | modifier le code] Galerie[modifier | modifier le code] Notes et références[modifier | modifier le code] Annexes[modifier | modifier le code]
Marc de café, l'or brun du jardinier Le marc de café est un excellent engrais naturel qui favorise la fertilité du sol, mais pas seulement ! Il possède également un effet répulsif pour certains insectes et ravageurs du jardin. Découvrez dans cet article, l’ensemble des usages qui permet l’utilisation du marc de café au jardin. Comment utiliser le Marc de café au jardin ? Vous pouvez soit l’incorporer superficiellement dans le sol, à proximité des végétaux. Le marc de café pour aider vos semis ! Bien sec, il se mélange aux graines fines pour bien répartir les semis, ce qui évitera des surcharges localisées, de plus grâce à sa couleur sombre, il vous permettra de bien délimiter votre semis. Un effet répulsif contre les nuisibles du jardin ! En le plaçant au pied des végétaux, le marc de café est un bon répulsif contre la mouche de la carotte ou encore celle du poireau, les nématodes des racines et empêche l’installation des pucerons. Le marc de café favorise le compost ! Vous avez aimé cet article ?
Khan Academy La structure de l'Arbre de Vie Le mot Sephirah (pluriel Sephiroth) désigne en hébreu une "émanation numérique". Qu'est-ce donc ? C'est l'idée de quelquechose engendré par autre chose, et dans un certain ordre. Ainsi, comme on vient de le voir, la Création de l'Univers a consisté en l'émanation successive de dix Sephiroth, depuis Kether, l'étincelle de vie divine, pour arriver à Malkut, le monde matériel. Les Sephiroth sont donc, dans l'ordre d'involution : Kether, Hokmah, Binah, Chesed, Geburah, Tipheret, Netzah, Hod, Yesod et Malkut. Cet ordre est dit "d'involution" car il est celui dans lequel l'univers a été créé. Venons-en maintenant à une ébauche de structure de l'Arbre de Vie. Olam Ha'Atziluth, le monde de l'émanation, regroupe Kether, Hokmah et Binah. Ce qu'il n'est pas forcément facile d'appréhender à priori dans ce regroupement par mondes, c'est que chaque monde est présent dans chaque Sephirah et inversement. Venons-en maintenant à un deuxième regroupement que l'on peut effectuer. Sohar, le Monde Parfait.
Flightradar24.com - Live flight tracker! In order to save data consumption Flightradar24 web page times out after 30 minutes. Please reload the web page to get another 30 minutes. or get a Flightradar24 Premium subscription and Flightradar24.com will not time-out again! Cours de mathématiques supérieures suivant: Propriétés de l'intégrale de monter: Calcul intégral précédent: Calcul intégral Sous-sections Le programme ne précise pas si la définition de l'intégrale de Riemann doit figurer dans le cours. Certains collègues commencent ce cours directement avec la définition de la primitive d'une fonction, et Ainsi, le théorème fondamental de l'analyse, qui établit le lien entre l'intégration et la dérivation, devient trivial. A mon avis, ce cours est quand même l'occasion ou jamais de définir l'intégrale de Riemann. Subdivisions et sommes de Darboux Définition Une subdivision d'ordre d'un intervalle est une partie finie telle que On notera l'ensemble des subdivisions de Exemple [subdivision équidistante] Lorsque avec , on parle de la subdivision équidistante d'ordre de ; on la note parfois . est le pas (uniforme) de cette subdivision. Définition La somme de Darboux inférieure resp. supérieure de relativement à une subdivision sont définies par où est la longueur du sous-intervalle est bornée, (entre et ) à pour .
Courbe de Peano Un article de Wikipédia, l'encyclopédie libre. Giuseppe Peano Une courbe de Peano est une courbe plane paramétrée par une fonction continue sur l'intervalle unité [0, 1], surjective dans le carré [0, 1]×[0, 1], c'est-à-dire que la courbe passe par chaque point du carré : elle « remplit l'espace ». Toutes ces courbes sont des fractales : bien que formées d'une simple ligne, elles sont de dimension 2. Ce type de courbes est nommé en l'honneur de Giuseppe Peano, qui fut le premier à en décrire une. Historique[modifier | modifier le code] Dans un article de 1890[1] Giuseppe Peano décrit une courbe auto-intersectante qui passe par tous les points de la surface du carré unité. vers le carré unité défini sur . La clé passe par l'élaboration d'une courbe nulle part différentiable. Peano utilise l'existence d'un développement en base trois pour tout nombre réel. et le couple de suites de la manière suivante : Quatre itérations de la courbe de Peano L'article de Peano ne contenait pas d'illustration.
Nombre d'or Un article de Wikipédia, l'encyclopédie libre. La proportion définie par et est dite d'« extrême et moyenne raison » lorsque est à ce que , soit : lorsque . est alors égal au nombre d'or. Le nombre d'or est une proportion, définie initialement en géométrie comme l'unique rapport entre deux longueurs telles que le rapport de la somme des deux longueurs ( ) sur la plus grande ( ) soit égal à celui de la plus grande ( ) sur la plus petite ( ) c'est-à-dire lorsque . Ce nombre irrationnel est l'unique solution positive de l'équation . soit approximativement[1] 1,6180339887. Il est érigé en théorie esthétique et justifié par des arguments d'ordre mystique, comme une clé importante, voire explicative, dans la compréhension des structures du monde physique, particulièrement pour les critères de beauté et surtout d'harmonie ; sa présence est alors revendiquée dans les sciences de la nature et de la vie, proportions du corps humain ou dans les arts comme la peinture, l'architecture ou la musique. , où
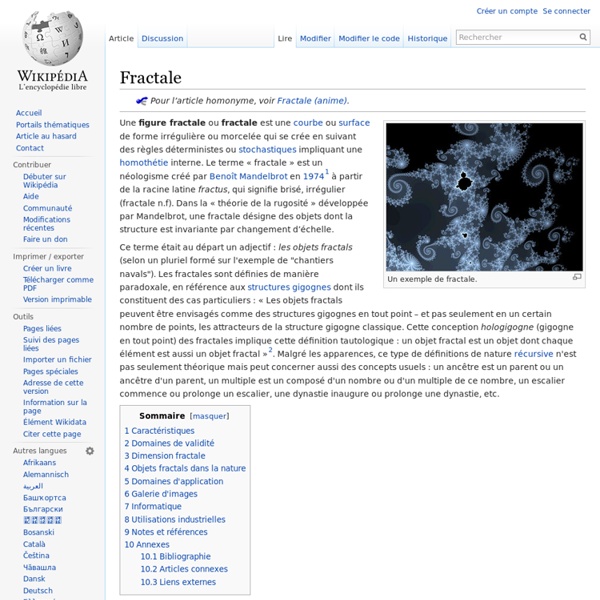
Arbre fractal ARBRE FRACTALFractal tree, Baum-Fraktal Un arbre est fractal en ce sens que ses branches maîtresses, issues du tronc, sont chacune des arbres en réduction. Pour simplifier, si le tronc est le segment [AB], nous allons considérer p similitudes fi transformant le segment [AB] en des segments plus courts [CiDi], attachés aux troncs (c'est-à dire que Ci appartient à [AB]). , qui converge vers l'attracteur des fi , lequel peut être considéré comme le "feuillage" de l'arbre : L'arbre est, lui, la réunion des Kn ; son feuillage est donc l'ensemble des extrémités de ses branches. Voici la construction animée des 10 premières étapes, avec des Ci égaux à B, et deux similitudes directes de rapport 0,7 et d'angles p/9 et -2p/9. Remarquons que l'arbre est formé de spirales logarithmiques approchées : et Si l'on veut obtenir l'arbre complet comme un attracteur, il faut rajouter une p + 1ème contraction. mais il possède la particularité d'avoir un feuillage égal à la courbe du C ; Ca, c'est un vrai !
Le siècle des Lumières : un héritage pour demain Dans l'Europe des Lumières se lèvent alors des hommes pour dénoncer et combattre l'esclavage. La révolte des esclaves dans la Jamaïque anglaise ainsi que dans les Guyanes françaises et surtout hollandaises donne un souffle à ce courant de pensée. Elle inspire à Voltaire, dans Candide, l'épisode du nègre de Surinam. À la veille de la Révolution, des sociétés anti-esclavagistes voient le jour, d'abord à Londres, puis à Paris, sous la forme de la société des Amis des noirs, fréquentée par les esprits éclairés et les révolutionnaires, parmi lesquels on compte, entre autres, Condorcet et Mirabeau. Abrogé par la Convention, en 1794, rétabli sous Napoléon, en 1802, l'esclavage dans les colonies françaises est définitivement aboli, sous la IIe République, grâce à Victor Schoelcher, en 1848.> entretien avec Plantu, auteur de bande dessinée
Arbre, classement des connaissances, l’arborescence du savoir L’idée de classer le savoir sur un arbre, comme on classe les membres d’une famille, se développe au XIIIè siècle, période-clé pour le classement du savoir : c’est à cette date, par exemple, que s’impose le classement alphabétique. Ce sont d’abord les connaissances théologiques (la science de Dieu) qui prennent cette forme nouvelle, et destinée à perdurer, de l’arborescence du savoir. Speculum virginum (1200) : base de l’arbre : allégorie de l’Orgueil tenant le calice d’or de Babylone ; six rameaux avec sept feuilles de part et d’autre du tronc, un rameau de douze feuilles au sommet, tous dirigés vers le bas ; à la base de chaque rameau, nom d’un vice : quatre rameaux du bas avec vices de l’esprit (tristesse, colère, envie, orgueil), trois rameaux du haut avec vices du plaisir matériel (dissipation, gourmandise, avarice) ; dans les feuilles, vices subsidiaires ; au sommet de l’arbre, Adam cachant sa nudité ; deux hybrides zoomorphes autour du tronc, deux mordant le rameau supérieur.
Echanger ses savoirs autour de l'Arbre L'essentiel est d'offrir et de donner. Ce principe de réciprocité est le moteur de l'association », précise Annie Vinet, vice-présidente de l'association saintaise, l'Arbre des savoirs (1). Créée en 1998, sur l'idée d'un employé municipal saintais qui voulait développer ce système au sein de son service, elle regroupe aujourd'hui, près de 120 membres qui ont un savoir à partager. En entrant dans le local de l'association, pas de doute sur la destination, l'Arbre des savoirs, c'est bien ici. Parmi les membres, Rose-Line, retraitée, vient assister au cours d'anglais, dispensé par Kate, une Britannique originaire de Bristol. « En ce moment, je '' reçois'' de l'anglais, indique la Saintaise, membre de l'association depuis plus de trois ans. En échange, Rose-Line « donne » une initiation à l'espagnol. Un vrai lien social L'heure d'anglais assurée par Kate a aussi attiré Victor, d'origine chilienne. « Cela fait au moins cinq ans que je viens, confie ce natif de Santiago.