La relativité restreinte expliquée en animation

Stellarium Classificazione Annuncio Pubblicitario Chiunque abbia qualche infarinatura di Biologia sa sicuramente che la classificazione degli organismi viventi è un’attività che da lungo tempo ormai coinvolge studiosi delle Scienze Naturali provenienti da tutto il mondo e dalle epoche più disparate. Tutti nel nostro percorso scolastico abbiamo studiato che in natura c’é differenza tra un Animale, una Pianta, un Fungo o un Batterio (e non solo a livello visivo-esteriore). Ci hanno detto che essi appartengono a categorie differenti, le cosiddette categorie tassonomiche, che ci permettono di distinguere gli organismi diversi tra loro e raggruppare invece quelli simili. Fin qui credo che tutti siamo d’accordo. Tuttavia, nel tempo numerose ricerche, basate soprattutto sullo studio del DNA e dei caratteri molecolari, hanno mostrato che in alcuni casi erano necessarie delle precisazioni e/o delle vere e proprie revisioni. La nascita della sistematica Nomenclatura binomia, trinomia e categorie tassonomiche Domini Regni

Le mystère du manuscrit de Voynich [2011] Espace Enseignants - Le chat de Schrödinger Intégrer ce média sur votre site Cosmic Inflation Explained Free excerpt from The PHD Movie 2! - Watch this free clip from the movie that Nature called "Astute, funny"! Watch the new movie! Summer Hiatus - PHD has been on Summer Hiatus while Jorge finishes the new PHD Movie. The PHD Movie 2 OFFICIAL TRAILER - is out!! Filming is done! Coming to Campuses this Fall! The Science Gap - Watch Jorge's TEDx Talk:

Trois lois de Clarke L'auteur de science-fiction Arthur C. Clarke a formulé les trois lois suivantes : Origine[modifier | modifier le code] Les lois de Clarke ont été proposées par Arthur C. Dans une révision de 1973 de Profiles of the Future, Clarke reconnut la deuxième loi et proposa la troisième dans le but d'en arrondir le nombre, ajoutant : « Comme les trois lois étaient suffisantes pour Newton, j'ai modestement décidé de m'arrêter là ». Parmi ces trois lois, la troisième est la plus connue et la plus citée : celle-ci codifie en effet ce qui est sans doute la plus significative de ses rares contributions formelles à la fiction spéculative. Références[modifier | modifier le code] ↑ (en) Arthur Charles Clarke, Profiles of the Future, 1973↑ Gregory Bendford, Fondation en péril, HarperPrism, 1997↑ (en) « The Deepening Paradox » [archive], sur kschroeder.com (consulté le 18 août 2014)

sciences & philosophies ascociées Chat de Schrödinger Le chat de Schrödinger est l’un des concepts scientifiques les plus souvent rencontrés dans la culture populaire mais les moins bien compris par le grand public. Rappelons en quelques mots l’expérience imaginée par Schrödinger : un chat est placé dans une boîte fermée aux côtés d’un petit échantillon de substance radioactive, choisie de telle sorte qu’il y a une chance sur deux que l’un de ses atomes se désintègre en l’espace d’une heure. Si c’est le cas, la désintégration est détectée par un compteur Geiger, ce qui active un petit marteau qui vient briser une fiole contenant un produit toxique et fait passer le chat de vie à trépas. L’essentiel est qu’au bout d’une heure, il y a une chance sur deux pour que rien ne se soit passé et que le chat soit encore en vie, et une chance sur deux pour qu’un atome se soit désintégré et que le chat ait été tué. Pour comprendre l’importance du « chat de Schrödinger », il convient de le situer dans son contexte historique. Auteur(s) : Franck Stevens

Time travellers: please don’t kill Hitler | Dean Burnett If you find yourself suddenly gaining access to a time machine, what’s the first thing you’d do? If you said “kill Adolf Hitler”, then congratulations; you’re a science-fiction character. Actually, the whole “access to a time machine” thing suggested that already, but the desire to kill Hitler clinches it. Any time-travelling sci-fi character (at least ones created by Western society) seems to want to kill Hitler, so much so that there’s a trope about how it’s impossible. That attempting to kill Hitler has become such a common sci-fi plot device speaks volumes. What about Stalin? It’s understandable. Ethical quandary Could you actually kill another human being? But let’s assume you are willing to kill one to save millions of others. Maybe later, when the Reich is in place but he hadn’t committed genocide yet. Wider context Problems rarely exist in isolation. Chaos theory Say whoever replaced him was ineffectual and the war ended with reduced loss of life and destruction. Cultural reference

Scientific Proof Is A Myth You've heard of our greatest scientific theories: the theory of evolution, the Big Bang theory, the theory of gravity. You've also heard of the concept of a proof, and the claims that certain pieces of evidence prove the validities of these theories. Fossils, genetic inheritance, and DNA prove the theory of evolution. The Hubble expansion of the Universe, the evolution of stars, galaxies, and heavy elements, and the existence of the cosmic microwave background prove the Big Bang theory. Except that's a complete lie. Reality is a complicated place. We also can't observe or measure everything. In order to come up with a model capable of predicting what will happen under a variety of conditions, we need to understand a few things. What we're capable of measuring, and to what precision. Our best theories, like the aforementioned theory of evolution, the Big Bang theory, and Einstein's General Relativity, cover all of these bases. This doesn't mean it's impossible to know anything at all.

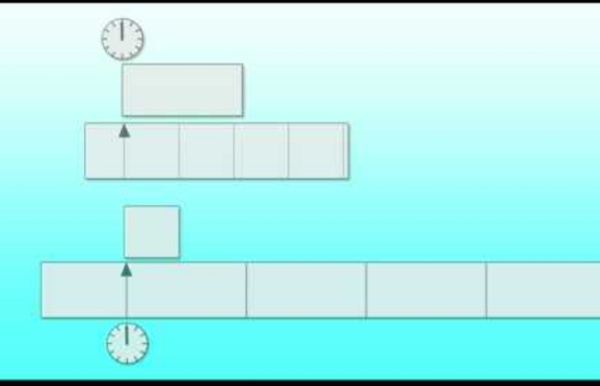
phisique A Slower Speed of Light Download the latest beta releases A Slower Speed of Light is a first-person game prototype in which players navigate a 3D space while picking up orbs that reduce the speed of light in increments. Custom-built, open-source relativistic graphics code allows the speed of light in the game to approach the player’s own maximum walking speed. Visual effects of special relativity gradually become apparent to the player, increasing the challenge of gameplay. Download our PowerPoint presentation about the relativistic effects in the game: PPT PPTX OpenRelativity A Slower Speed of Light was created using OpenRelativity, an open-source toolkit for the Unity game development environment. Requirements A Slower Speed of Light has been tested on computers with the configurations listed below. Intel Core 2 Duo T9900 or Core i7 (2.8GHz clock speed)Windows 7, Mac OS X 10.6.8 (Snow Leopard) or higher, and Linux (Ubuntu 13)AMD Radeon HD 6970M/AMD Mobility Radeon HD 4850/Nvidia GeForce 9600M GT8GB RAM Posters