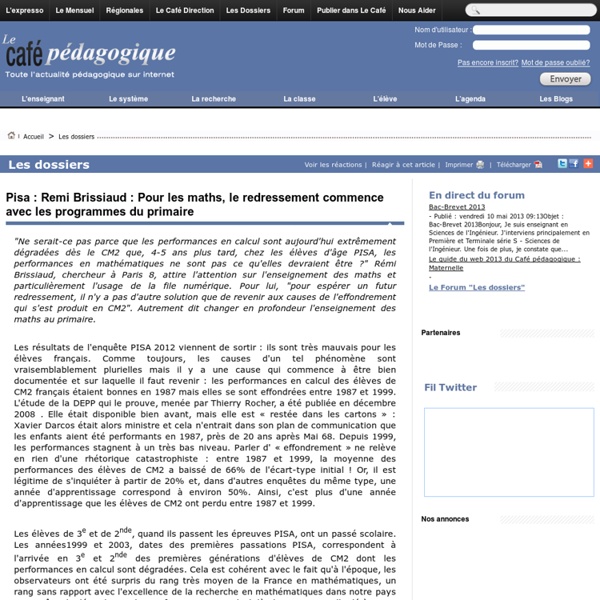
Jeu Flexibitiz (pour l’entraînement de la subitisation et de la flexibilité mentale)
Jeu Flexibitiz (pour l’entraînement de la subitisation et de la flexibilité mentale) rsam logopédie, Matériel, Orthophonie cartes, flexibilité mentale, Flexibitiz, jeu, jeux, logico-mathématiques, Stanislas Dehaene, subitisation, subitizing Présentation Il s’agit d’un jeu de 54 cartes (6 planches) comprenant des collections de disques de couleurs différentes. Exemple de cartes du jeu Flexibitiz Le jeu s’inspire des règles d’une bataille Corse ou du Jungle Speed®. Pour deux joueurs : - si un joueur se trompe et tape alors que les deux cartes n’ont pas le même cardinal, son adversaire gagne les cartes au milieu de la table. Pour plus de deux joueurs : - si un joueur se trompe, il est "glacé" et ne peut plus joueur jusqu’à la fin du tour c’est-à-dire quand l’un des joueurs remportent les cartes au milieu de la table. Objectifs Public En séance et dans le cadre d’un travail sur la flexibilité mentale, n’hésitez pas à jouer sur les "feintes" (faire semblant de taper) pour travailler l’inhibition.
ONL
Document Actions Cette rubrique Livres de jeunesse et apprentissages se situe en prolongement des principes énoncés dans Livres et apprentissages à l’école, ONL, publication Scéren / Savoir Livre (1999, première édition - 2003, édition actualisée). Elle propose une démarche d'entrée « en constellation » dans l’univers des livres et sélectionne, par ailleurs, des titres pour chacun des trois cycles, à partir de critères explicites définissant les apprentissages engagés. Vous trouverez ici des exemples, des explicitations et une mise en œuvre de la démarche affichée, à travers une présentation didactique et appliquée. En débatL'équipe de travail est coordonnée par :, Secrétaire générale de l’ONL, , Chargé de mission.
La psychologie cognitive et l’école > Vous êtes un professionnel : Enfant en difficult s scolaires Lyon - Psychologie cognitive Lyon - Cabinet BAK & associ s Lyon | Psychologie cognitive
Comprendre et résoudre les difficultés scolaires Le développement de la pensée d'un individu va se structurer d'une façon de plus en plus mobile à travers des échanges constants avec l'environnement. L'école va solliciter les structures opératoires que devrait utiliser tout enfant ayant une capacité d'anticipation. Les enfants qui présentent certaines difficultés en mathématiques, en orthographe, ont une pensée très rigide. En parvenant à organiser ses actions, l'enfant ou l'adolescent en fin de remédiation, sera en mesure d'avoir une maîtrise de la réalité, ce qui impliquera un intérêt grandissant pour des éléments de plus en plus abstraits et diversifiés. Les enfants en difficultés scolaires ne se comptent plus, tant ils sont nombreux. La seconde partie du problème se situe au niveau de leurs structures cognitives, de leur degré d'élaboration et d'organisation de la réalité. Ainsi, le processus cognitif que nous venons de décrire est complété par l'accommodation.
Apprendre les tables de multiplication
Présentation des applications Dans la série des applications pour TBN, vidéoprojecteur et compagnie, je vous propose de découvrir quatre d’entre elles pour apprendre les tables de multiplication. Afficher une table à l’écran en deux clics, associer les schèmes correspondants, afficher les réponses ou compléter les résultats… Yapluka! Après avoir téléchargé et décompressé le fichier ZIP, vous accédez à un dossier qui contient quatre applications: Les tablesLe tableau à double entréesLes associationsLe défi Pour chacune d’elles, vous disposez d’un panneau de contrôle pour choisir parmi les différentes options disponibles. Les tables de multiplication En quelques clics, il vous est possible de présenter la table de multiplication de votre choix dans l’ordre ou dans le désordre. Le tableau à double entrées Sur le même principe mais avec un tableau à double entrées, cette application permet de présenter toutes les tables de multiplication en un seul affichage. Les associations Le défi Remarques
Académie de Mayotte
Quelles pratiques pédagogiques faut-il éviter à l’école maternelle et au CP ? Les réponses d’une expérimentation menée à l’échelle de la nation
Rémy Brissiaud Maître de conférence de psychologie Université Paris 8, Laboratoire Paragraphe Des chercheurs de la DEPP (note 08.38 de décembre 2008) ont comparé les performances en 1987, 1999 et 2007 d’un échantillon représentatif des élèves de CM2, en s’appuyant sur les items communs aux différentes passations pour rendre la comparaison possible. Certaines causes peuvent être écartées a priori. Entre 1970 et 1986 : la période des activités pré-numériques On doutait à l’époque que les enfants puissent profiter d’un enseignement des nombres avant 6-7 ans et, à l’école maternelle, l’accent était mis sur des activités qualifiées de « pré-numériques ». Au CP, l’année commençait elle aussi par des activités pré-numériques. Quiconque prenant connaissance de ces informations concernant l’école en France entre 1970 et 1986, s’écrierait : « Avec un enseignement aussi tardif, les élèves ne devaient pas devenir très forts en calcul ! Pourquoi une telle dégradation : la notion de comptage-numérotage
Eduscol les intelligences multiples
La théorie des Intelligences multiples d'Howard Gardner La notion d' « Intelligences multiples » a été proposée par un professeur de l'Université de Harvard, Howard Gardner, en 1983 dans son livre Frames of Minds : the Theory of Multiple Intelligence. Il suggère que chaque individu dispose de plusieurs types d'intelligences, pour lesquelles il a naturellement une plus ou moins grande compétence. L'intelligence corporelle / kinesthésique C'est la capacité à utiliser son corps d'une manière fine et élaborée, à s'exprimer à travers le mouvement, à être habile avec les objets. L'utilisation de la théorie des Intelligences multiples ne vise pas, bien sûr, à classifier les individus selon un seul type d'intelligence et à les enfermer dans des catégories et exclusives. L'expérimentation à l'école maternelle des Hauldres Mise en œuvre Exemples d'ateliers proposés dans la salle des intelligences : L'exemple d'une séquence en grande section Exemples d'ateliers : Pour les élèves Pour les enseignants
Le nombre à l’école maternelle : des changements en vue, mais dans quel sens ?
Devant la perspective de changements dans les programmes en maternelle, Rémi Brissiaud, maître de conférences de psychologie à l'Université de Cergy-Pontoise, revient sur les « premiers pas en mathématiques », sur les façons de les enseigner, et se livre à une analyse critique des recommandations de S. Dehaene. Mardi 13 mars, une conférence nationale sur l’enseignement des mathématiques à l’école et au collège s’est tenue à Lyon. Elle a été préparée par des auditions d’« experts » (dont l’auteur de ces lignes). Chaque audition a été prolongée par l’écriture d’un texte mis en ligne sur le site educmath[i]. Dans leur contribution, Philippe Claus et Jean-Louis Durpaire[ii], inspecteurs généraux, écrivent qu’il conviendrait de réexaminer les « premiers pas en mathématiques ». Pour le savoir, il est instructif d’étudier le contenu d’une des interventions lors de la conférence : celle de Stanislas Dehaene, professeur au collège de France en neurosciences. Éviter le comptage mécanique S. S. S.