


Trigonometry Trigonometry (from Greek trigonon "triangle" + metron "measure") Want to learn Trigonometry? Here is a quick summary. Trigonometry helps us find angles and distances, and is used a lot in science, engineering, video games, and more! Right-Angled Triangle The triangle of most interest is the right-angled triangle. Another angle is often labeled θ, and the three sides are then called: Adjacent: adjacent (next to) the angle θ Opposite: opposite the angle θ and the longest side is the Hypotenuse Why? Why is this triangle so important? Imagine we can measure along and up but want to know the direct distance and angle: Or we have a distance and angle and need to "plot the dot" along and up: Questions like these are common in engineering, computer animation and more. And trigonometry gives the answers! Sine, Cosine and Tangent The main functions in trigonometry are Sine, Cosine and Tangent They are simply one side of a right-angled triangle divided by another. For any angle "θ": sin(45°) = 0.7071... Done!
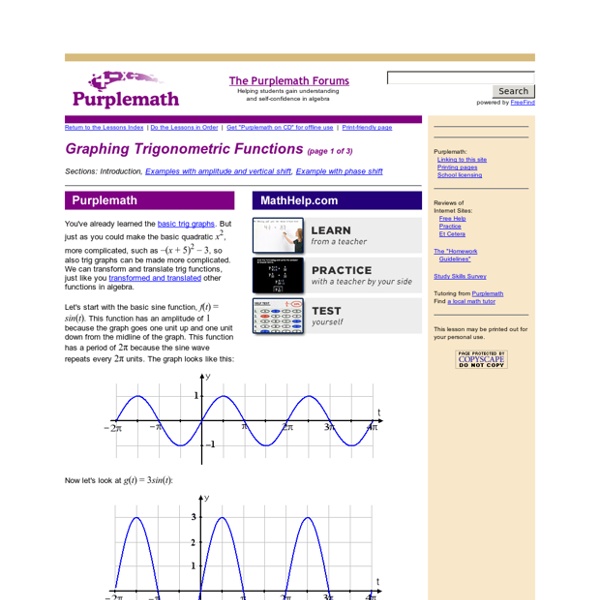
Basic Trigonometric Graphs Trigonometric Functions and Their Graphs: The Sine and Cosine (page 1 of 3) Sections: The sine and cosine, The tangent, The co-functions At first, trig ratios related only to right triangles. Then you learned how to find ratios for any angle, using all four quadrants. Then you learned about the unit circle, in which the value of the hypotenuse was always r = 1 so that sin(θ) = y and cos(θ) = x. In other words, you progressed from geometrical figures to a situation in which there was just one input (one angle measure, instead of three sides and an angle) leading to one output (the value of the trig ratio). Looking at the sine ratio in the four quadrants, we can take the input (the angle measure θ), "unwind" this from the unit circle, and put it on the horizontal axis of a standard graph in the x,y-plane. As you can see, the height of the red line, being the value of sin(θ) = y, is the same in each graph. The Sine Wave When you do your sine graphs, don't try to plot loads of points.
Lesson HOW TO - Solve Trigonometric equations Introduction The solution of trigonometric equations is one topic that students have particular problems with. There are a few reasons for this: 1. there is usually a simplify part first that requires use of some TRIG identities. 2. there is the use of RADIANS rather than degrees, for which some students are not at ease with. 3. there is the repetitive aspect of TRIG functions that students find bewildering. All in all, a potentially daunting topic. To be honest though, there is nothing that you need fear here, so long as you take it methodically and slowly. Solving the TRIG Equation Of the 3 topics listed above, I am concentrating on part 3, here in this Lesson. First thing, when solving a TRIG equation, is to understand or accept that each of SINE, COSINE and TANGENT have 2 angles that will satisfy the given equation within any 360 degree range. If we have multiples, such as cos(2x), then we also multiply up the possible number of solutions. Quadrant 1 is the top right one. Done! 1.
SOLVING TRIGONOMETRIC EQUATIONS Note: If you would like a review of trigonometry, click on trigonometry. Example 1: Solve for x in the following equation. There are an infinite number of solutions to this problem. First isolate the cosine term. To solve for x, we have to isolate x. How do we isolate the x? Let's restrict the domain so the function is one-to-one on the restricted domain while preserving the original range. If we restrict the domain of the cosine function to that interval , we can take the arccosine of both sides of each equation. The angle x is the reference angle. Therefore, if , then The period of equals and the period of , this means other solutions exists every units. where n is an integer. The approximate values of these solutions are You can check each solution algebraically by substituting each solution in the original equation. You can also check the solutions graphically by graphing the function formed by subtracting the right side of the original equation from the left side of the original equation.
Amplitude, Period, Phase Shift and Frequency Some functions (like Sine and Cosine) repeat forever and are called Periodic Functions. The Period is the length from one peak to the next (or from any point to the next matching point): The Amplitude is the height from the center line to the peak (or to the trough). The Phase Shift is how far the function is horizontally to the right of the usual position. The Vertical Shift is how far the function is vertically from the usual position. All Together Now! We can have all of them in one equation: y = A sin(Bx + C) + D amplitude is A period is 2π/B phase shift is −C/B vertical shift is D Example: sin(x) This is the basic unchanged sine formula. So amplitude is 1, period is 2π, there is no phase shift or vertical shift: Example: 2 sin(4x − 2) + 3 amplitude A = 2 period 2π/B = 2π/4 = π/2 phase shift −C/B = −(−2)/4 = 1/2 vertical shift D = 3 In words: Note the Phase Shift formula −C/B has a minus sign: Sometimes we have t instead of x (or maybe other variables): Example: 3 sin(100t + 1) And we get:
Unit Circle The "Unit Circle" is a circle with a radius of 1. Being so simple, it is a great way to learn and talk about lengths and angles. The center is put on a graph where the x axis and y axis cross, so we get this neat arrangement here. Sine, Cosine and Tangent Because the radius is 1, we can directly measure sine, cosine and tangent. What happens when the angle, θ, is 0°? cos 0° = 1, sin 0° = 0 and tan 0° = 0 What happens when θ is 90°? cos 90° = 0, sin 90° = 1 and tan 90° is undefined Try It Yourself! Have a try! The "sides" can be positive or negative according to the rules of Cartesian coordinates. Also try the Interactive Unit Circle. Pythagoras Pythagoras' Theorem says that for a right angled triangle, the square of the long side equals the sum of the squares of the other two sides: x2 + y2 = 12 But 12 is just 1, so: x2 + y2 = 1 (the equation of the unit circle) Also, since x=cos and y=sin, we get: (cos(θ))2 + (sin(θ))2 = 1 a useful "identity" Important Angles: 30°, 45° and 60° How To Remember?
Chapter 5: Trigonometric Functions<BLURT> Chapter 5: Trigonometric Functions 1. Please solve 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. Copyright ©2001 The McGraw-Hill Companies. Algebra/Trig Review - Solving Trig Equations Solve the following trig equations. For those without intervals listed find ALL possible solutions. For those with intervals listed find only the solutions that fall in those intervals. There’s not much to do with this one. So, we are looking for all the values of t for which cosine will have the value of . From quick inspection we can see that is a solution. . To find this angle for this problem all we need to do is use a little geometry. with the positive x-axis, then so must the angle in the fourth quadrant. , but again, it’s more common to use positive angles so, we’ll use We aren’t done with this problem. that we want for the solution and sometimes we will want both (or neither) of the listed angles. This is very easy to do. to represent all the possible angles that can end at the same location on the unit circle, i.e. angles that end at . then rotate around in the counter-clockwise direction (n is positive) or clockwise direction (n is negative) for n complete rotations. by using on .
Amplitude and Period Amplitude and Period Learning Objective(s) · Understand amplitude and period. · Graph the sine function with changes in amplitude and period. · Graph the cosine function with changes in amplitude and period. · Match a sine or cosine function to its graph and vice versa. You know how to graph the functions and . or , where a and b are constants. We used the variable previously to show an angle in standard position, and we also referred to the sine and cosine functions as . for the input (as well as to label the horizontal axis). . You know that the graphs of the sine and cosine functions have a pattern of hills and valleys that repeat. . (or ) on the interval looks like the graph on the interval . The graph below shows four repetitions of a pattern of length . is on the interval is one cycle. You know from graphing quadratic functions of the form that as you changed the value of a you changed the “width” of the graph. and see how changes to b will affect the graph. periodic, and if so, what is the period?
Section 4: Sine And Cosine Rule These examples illustrate the decision-making process for a variety of triangles: SOLVING TRIGONOMETRIC EQUATIONS Note: If you would like an review of trigonometry, click on trigonometry. Solve for x in the following equation. Example 1: There are an infinite number of solutions to this problem. To solve for x, you must first isolate the sine term. If we restriction the domain of the sine function to , we can use the inverse sine function to solve for reference angle 3x and then x. We know that the e function is positive in the first and the second quadrant. that terminates in the second quadrant. The solutions are and The period of the function is This means that the values will repeat every radians in both directions. where n is an integer. The approximate solutions are These solutions may or may not be the answers to the original problem. Numerical Check: Check the answer x=0.174532925 Left Side: Right Side: Since the left side equals the right side when you substitute 0.174532925for x, then 0.174532925 is a solution. Check the answer x=0.872665 Since the left side equals the right side when you substitute
Trigonometric questions Answer for Worksheet