

Wood Turned Art inspired by Minimal Surfaces Math. Breezy Hill Turning Turned Wood Art by Michael Foster Hide Menu Minimal Surfaces I have recently been exploring the intersection of math and sculpture.

One of the really cool things that I have discovered is the class of math objects called minimal surfaces. . © 2011 Michael Foster Contact Me.
Alan Schoen geometry. Reflections concerning triply-periodic minimal surfaces. In recent decades, there has been an explosion in the number and variety of embedded triply-periodic minimal surfaces (TPMS) identified by mathematicians and materials scientists.

Only the rare examples of low genus, however, are commonly invoked as shape templates in scientific applications. Exact analytic solutions are now known for many of the low genus examples. The more complex surfaces are readily defined with numerical tools such as Ken Brakke's Surface Evolver software [1] or Holyst and Góźdź's Landau–Ginzburg model [2]. Even though table-top versions of several TPMS have been placed within easy reach by rapid prototyping methods, the inherent complexity of many of these surfaces makes it challenging to grasp their structure.
The problem of distinguishing TPMS, which is now acute because of the proliferation of examples, has been addressed by Eric Lord and Alan Mackay [3]. Table 1. Figure 1. Large interstitial sites (red) in the diamond crystal structure (green) (stereo image). Stretched grid method. The stretched grid method (SGM) is a numerical technique for finding approximate solutions of various mathematical and engineering problems that can be related to an elastic grid behavior.
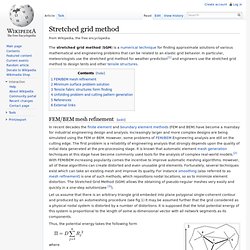
In particular, meteorologists use the stretched grid method for weather prediction[1] and engineers use the stretched grid method to design tents and other tensile structures. FEM/BEM mesh refinement[edit] In recent decades the finite element and boundary element methods (FEM and BEM) have become a mainstay for industrial engineering design and analysis. Increasingly larger and more complex designs are being simulated using the FEM or BEM. However, some problems of FEM/BEM Engineering analysis are still on the cutting edge. Let us assume that there is an arbitrary triangle grid embeded into plane polygonal single-coherent contour and produced by an automeshing procedure (see fig.1) It may be assumed further that the grid considered as a physical nodal system is distorted by a number of distortions.
And. Minimal surface. A helicoid minimal surface formed by a soap film on a helical frame In mathematics, a minimal surface is a surface that locally minimizes its area.
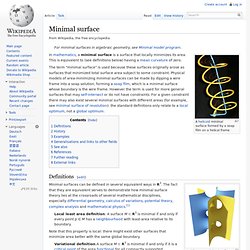
This is equivalent to (see definitions below) having a mean curvature of zero. The term "minimal surface" is used because these surfaces originally arose as surfaces that minimized total surface area subject to some constraint. Physical models of area-minimizing minimal surfaces can be made by dipping a wire frame into a soap solution, forming a soap film, which is a minimal surface whose boundary is the wire frame. However the term is used for more general surfaces that may self-intersect or do not have constraints. Definitions[edit] Saddle tower minimal surface. Minimal surfaces can be defined in several equivalent ways in R3. Note that this property is local: there might exist other surfaces that minimize area better with the same global boundary. This definition makes minimal surfaces a 2-dimensional analogue to geodesics. History[edit]
Helicoid?