

Tabula rasa. The term also is used as the name of an epistemological theory that individuals are born without built-in mental content and that all of their knowledge comes from experience and perception.
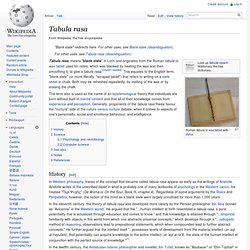
Arithmometer. Arithmomètre built by Louis Payen around 1887 The Arithmometer or Arithmomètre was the first digital mechanical calculator strong enough and reliable enough to be used daily in an office environment.
This calculator could add and subtract two numbers directly and could perform long multiplications and divisions effectively by using a movable accumulator for the result. Patented in France by Thomas de Colmar in 1820 and manufactured from 1851 to 1915, it became the first commercially successful mechanical calculator.[1] Its sturdy design gave it a strong reputation of reliability and accuracy[2] and made it a key player in the move from human computers to calculating machines that took place during the second half of the 19th century.[3] Its production debut of 1851 launched the mechanical calculator industry[1] which ultimately built millions of machines well into the 1970s.
Evolution[edit] Searching for a Solution: 1820-1851[edit] Detail of an arithmometer built before 1851. Legacy[edit] Mayan Mathematics. The Mayan civilisation had settled in the region of Central America from about 2000 BC, although the so-called Classic Period stretches from about 250 AD to 900 AD.

At its peak, it was one of the most densely populated and culturally dynamic societies in the world. The importance of astronomy and calendar calculations in Mayan society required mathematics, and the Maya constructed quite early a very sophisticated number system, possibly more advanced than any other in the world at the time (although the dating of developments is quite difficult). The Mayan and other Mesoamerican cultures used a vigesimal number system based on base 20 (and, to some extent, base 5), probably originally developed from counting on fingers and toes. The numerals consisted of only three symbols: zero, represented as a shell shape; one, a dot; and five, a bar.
Thus, addition and subtraction was a relatively simple matter of adding up dots and bars. Indian Mathematics. Despite developing quite independently of Chinese (and probably also of Babylonian mathematics), some very advanced mathematical discoveries were made at a very early time in India.

Mantras from the early Vedic period (before 1000 BC) invoke powers of ten from a hundred all the way up to a trillion, and provide evidence of the use of arithmetic operations such as addition, subtraction, multiplication, fractions, squares, cubes and roots. A 4th Century AD Sanskrit text reports Buddha enumerating numbers up to 1053, as well as describing six more numbering systems over and above these, leading to a number equivalent to 10421. Given that there are an estimated 1080 atoms in the whole universe, this is as close to infinity as any in the ancient world came. Sumerian/Babylonian Mathematics. Sumer (a region of Mesopotamia, modern-day Iraq) was the birthplace of writing, the wheel, agriculture, the arch, the plow, irrigation and many other innovations, and is often referred to as the Cradle of Civilization.

The Sumerians developed the earliest known writing system - a pictographic writing system known as cuneiform script, using wedge-shaped characters inscribed on baked clay tablets - and this has meant that we actually have more knowledge of ancient Sumerian and Babylonian mathematics than of early Egyptian mathematics. Indeed, we even have what appear to school exercises in arithmetic and geometric problems.
Chinese Mathematics. Even as mathematical developments in the ancient Greek world were beginning to falter during the final centuries BCE, the burgeoning trade empire of China was leading Chinese mathematics to ever greater heights.

The simple but efficient ancient Chinese numbering system, which dates back to at least the 2nd millennium BCE, used small bamboo rods arranged to represent the numbers 1 to 9, which were then places in columns representing units, tens, hundreds, thousands, etc. It was therefore a decimal place value system, very similar to the one we use today - indeed it was the first such number system, adopted by the Chinese over a thousand years before it was adopted in the West - and it made even quite complex calculations very quick and easy. Islamic Mathematics. The Islamic Empire established across Persia, the Middle East, Central Asia, North Africa, Iberia and parts of India from the 8th Century onwards made significant contributions towards mathematics.

They were able to draw on and fuse together the mathematical developments of both Greece and India. One consequence of the Islamic prohibition on depicting the human form was the extensive use of complex geometric patterns to decorate their buildings, raising mathematics to the form of an art. In fact, over time, Muslim artists discovered all the different forms of symmetry that can be depicted on a 2-dimensional surface. Prehistoric Mathematics. Our prehistoric ancestors would have had a general sensibility about amounts, and would have instinctively known the difference between, say, one and two antelopes.

But the intellectual leap from the concrete idea of two things to the invention of a symbol or word for the abstract idea of "two" took many ages to come about. Even today, there are isolated hunter-gatherer tribes in Amazonia which only have words for "one", "two" and "many", and others which only have words for numbers up to five.