

A Few Hypercomplex Onions. C# Generic Limitations The C# class Onion (listing below) allows experimentation with any of the Cayley-Dickson algebras mentioned in the previous related article, from the monodimensional reals, right up to the 512-dimensional austons :-) and beyond.
Modern professional libraries for this purpose still tend to be based on technologies like C++ templates, allowing for type variation in the underlying coefficients. And not just between a few integer and floating point types. Colombo , Sabadini , Struppa , Vajiac , Vajiac : Singularities of functions of one and several bicomplex variables. Hyper-Complex Numbers in Physics. Vlad L.

Negulescu Correspondence to: Vlad L. Negulescu , . Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved. Abstract The mathematical model and calculus with Hyper-Complex Numbers are extensively presented. The hit problem for the Dickson algebra – Site Title. In mathematics, the Cayley–Dickson construction, named after Arthur Cayley and Leonard Eugene Dickson, produces a sequence of algebras over the field of real numbers, each with twice the dimension of the previous one.

The algebras produced by this process are known as Cayley–Dickson algebras. They are useful composition algebras frequently applied in mathematical physics. The Cayley–Dickson construction defines a new algebra similar to the direct sum of an algebra with itself, with multiplication defined in a specific way (different from the multiplication provided by the genuine direct sum) and an involution known as conjugation. Tribonacci and Tribonacci-Lucas Sedenions. Visualizing a Theory of Everything! For Lisi’s latest ideas on a “Lie Group Cosmology (LGC)” ToE, see Be warned, it is over 40 heavy pages.
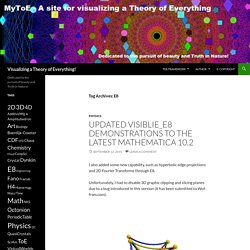
He also posted a new projection on FB. Sedenion — Wikipedia Republished. In abstract algebra, the sedenions form a 16-dimensional noncommutative and nonassociative algebra over the reals; they are obtained by applying the Cayley–Dickson construction to the octonions, and as such the octonions are a subfield of the sedenions.
Unlike the octonions, the sedenions are not an alternative algebra. Applying the Cayley–Dickson construction to the sedenions yields a 32-dimensional algebra, sometimes called the 32-ions or Trigintaduonions.[1] It is possible to apply the Cayley–Dickson construction to the sedenions infinitely often. The term sedenion is also used for other 16-dimensional algebraic structures, such as a tensor product of two copies of the biquaternions, or the algebra of 4 by 4 matrices over the reals, or that studied by Smith (1995). YouTube Encyclopedic 1/5Views:54 374151 247542 69213 9152 151 ✪ Hypercomplex numbers | Math History | NJ Wildberger✪ 0,999... = 1 ?! Arithmetic. Sedenions. Basic Algebra: The word sedenion is derived from sexdecim, meaning sixteen.

A sedenion is a hypercomplex number constituted from 16 basal elements. A set of sedenions form an algebra, S. Birth of Compound Numbers. 1.
Introduction It is observed and explained with several examples in [16], with rigorous analysis and justifications, that most of the simple and useful results, equalities, identities, formulas, laws, rules etc. which are frequently practiced at secondary school level of mathematics or higher level are not valid (i.e. can not be verified) in groups, rings, modules, fields, linear spaces, algebra over a field, associative algebra over a field, division algebra or in any existing standard algebraic system, in general, by virtue of their own characteristic properties only. This is a major gap and/or incompleteness in the existing literatures while regarding ‘Algebra’ as a subject. This invokes us to discover the exact minimum algebra which has the potential to provide a complete and sound platform in this sense. 2. Algebra is regarded as one of the most beautiful branches of mathematics and it is about finding the unknowns.
Note 2.1. Table 12 from Subalgebras of the Split Octonions. Abstract algebra - Rings with noncommutative addition. A new approach on electromagnetism with dual number coefficient octonion algebra. [1702.08657] Dual Horadam Octonions. Why not SEDENIONS? What ARE Clifford Algebras and Spinors? Tony Smith's Home Page What ARE Clifford Algebras ?

Why do I like Clifford Algebras? Chris Tickle, in August 2001, asked me about Clifford algebras: "... What would be the first thing you would tell me, what would be the first example you would show me,and what would be the first application you would show me? ... ". The first "application" would be thatCl(2) is 4-dimensional (it is the quaternions),butits graded structure is 1 2 1 The first 1 (called grade 0) is the scalars(here I am working with real numbers as scalars).
Dynkin diagram. Pictoral representation of symmetry The main interest in Dynkin diagrams is as a means to classify semisimple Lie algebras over algebraically closed fields.
This gives rise to Weyl groups, i.e. to many (although not all) finite reflection groups. Dynkin diagrams may also arise in other contexts. The term "Dynkin diagram" can be ambiguous. List of simple Lie groups. In mathematics, the simple Lie groups were first classified by Wilhelm Killing and later perfected by Élie Cartan.
This classification is often referred to as Killing-Cartan classification. The list of simple Lie groups can be used to read off the list of simple Lie algebras and Riemannian symmetric spaces. Tevian Dray - Subalgebras of the Split Octonions - JMM2018 AMS Quaternion Special Session. Linear algebra - Octonions in Mathematica - Mathematica Stack Exchange. By using our site, you acknowledge that you have read and understand our Cookie Policy, Privacy Policy, and our Terms of Service. Mathematica Stack Exchange is a question and answer site for users of Wolfram Mathematica. It only takes a minute to sign up. Sign up to join this community. From Wolfram MathWorld. Coxeter Planes. Warning: The discussion below is aimed at experts.
If you want a more down-to-earth explanation, read What's the E8 Picture? More Coxeter plane projections are available. Let c be a Coxeter element of some finite Weyl group W. Quaternions and Dual Quaternion Skinning · Gazoo.vrv. A Kind Of Magic. By Leron Borsten and Alessio Marrani Our journey starts in the fall of 1843 at the Dunsink Observatory[1], presiding from its hill-top vantage over the westerly reaches of Dublin City, seat to the then Astronomer Royal Sir William Rowan Hamilton.
In the preceding months Hamilton had become preoccupied by the observation that multiplication by a complex phase induces a rotation in the Argand plane, revealing an intimate link between two-dimensional Euclidean geometry and the complex numbers ℂ. Fascinated by this unification of geometry and algebra, Hamilton set about the task of constructing a new number system that would do for three dimensions what the complexes did for two.
Leron Borsten (left) and Alessio Marrani (right) stood before Hamilton’s fundamental relations, Broome bridge Dublin. Leron is currently a Schrödinger Fellow in the School of Theoretical Physics, Dublin Institute for Advanced Studies. Simple Lie Group. Is there a third dimension of numbers? Trinonions, Quaternions, Quinonions, Sextonions, Septonions, Octonions. The main thing to know in this area is Hurwitz theorem and Frobenius theorem which are the results that characterize R algebras (actually more) with certain properties. The former says that composition algebras have dimension 1,2,4 or 8, resulting in the reals, complexes, quaternions and octonions respectively. The latter is a subcase asking about division algebras instead, and it says the only dimensions are 1,2,4, (no octonions.)
Beyond that, if you're not asking for any special properties, there are R algebras of every dimension, and people are going to name them whatever they please. I know for sure about the sedenions, which are arrived at by a process analogous to passing up through the chain R⊆C⊆H⊆O. 21,617 Search Results - Keywords(subalgebras) Main. Circular and hyperbolic quaternions, octonions, and sedenions—Further results. Circular and hyperbolic quaternions, octonions, and sedenions—Further results. Mathoma. IUCAA Library. Toward the E8 code. David Madore. The beauty of E8. FQXi. From Hamilton’s Quaternions to Graves & Cayley’s Octonions – Louis Kauffman. Tevian Dray - Subalgebras of the Split Octonions - JMM2018 AMS Quaternion Special Session. MrCati. C ∗ -ternary 3-derivations on C ∗ -ternary algebras.
AIM math: Representations of E8. What is E8? What is E8? Asymptotia. Binary - Why do division algebras always have a number of dimensions which is a power of $2$? Have you ever seen this bizarre commutative algebra? I have encountered very strange commutative nonassociative algebras without unit, over a characteristic zero field, and I cannot figure out where do they belong. Has anybody seen these animals in any context? Octonions - Unital nonalternative real division algebras of dimension 8. How can the Cayley table for the elements of basis of a Cayley-Dickson algebra be summarized in an algebraic expression? Cayley-Dickson algebras and loops. Octonions and sedenions. Octonion. SmartMathLibrary - CodePlex Archive. Project DescriptionThe SmartMathLibrary brings scientific computing to the .NET platform. (3) How cool are octonions (8d numbers) for physics and why? C++ - Rotating vector3 by a quaternion.
Cohl Furey.
A Few Hypercomplex Numbers. Adam's Apples Adam learned to count sitting at home. Various number systems occurred to him, each one seeming to answer still more new questions... A Few Hypercomplex Onions. The Octonion Math That Could Underpin Physics. After breaks from school spent ski-bumming, bartending abroad and intensely training as a mixed martial artist, Furey later met the division algebras again in an advanced geometry course and learned just how peculiar they become in four strokes. Understanding A 10 Dimensional Universe. When someone mentions “different dimensions,” we tend to think of things like parallel universes — alternate realities that exist parallel to our own, but where things work or happened differently.
Dimensions and Multiverse. Higher dimensions in Mathmatics. Quaternion. Related Topics: Euler's Equation Quaternion is a geometrical operator to represent the relationship (relative length and relative orientation) between two vectors in 3D space.
Evernote shared notebook: