

SCIENCES Archives. Accueil. Le nombre "e" Hawking et le multivers : et le buzz revient... Bis repetita...
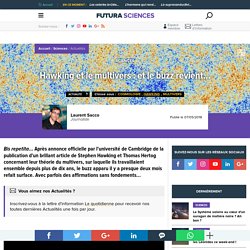
Après annonce officielle par l'université de Cambridge de la publication d'un brillant article de Stephen Hawking et Thomas Hertog concernant leur théorie du multivers, sur laquelle ils travaillaient ensemble depuis plus de dix ans, le buzz apparu il y a presque deux mois refait surface. Avec parfois des affirmations sans fondements... Interview : les théories sur les multivers sont-elles scientifiques ? Le concept du multivers, après avoir alimenté la science-fiction et le cinéma, infiltre le milieu de la physique théorique. Et s'il existait d’autres univers que le nôtre, différents ou identiques ? Stephen Hawking est décédé le 14 mars 2018. Les deux chercheurs avaient déposé depuis juillet 2017 sur arXiv, la célèbre archive en accès libre de la communauté scientifique globale, le dernier fruit de leur travail ainsi que les corrections successives au cours des mois qui allaient suivre.
La publication d'Hawking et Hertog indique des pistes mais pas de preuves. The Humanity Star. Conjecture de Syracuse 3n+1 - Collatz - Logiciel en Ligne. Rechercher un outil Conjecture de Syracuse Outil pour tester la conjecture de Collatz et variantes.

La conjecture de Syracuse (ou Collatz) propose de réaliser successivement les opérations de division par 2 à un nombre si il est pair, sinon le multiplier par 3 et ajouter 1. La conjecture stipule que la suite se termine par 1. Résultats Conjecture de Syracuse - dCode Catégorie(s) : Mathématiques, Fun dCode et vous dCode est gratuit et ses outils sont une aide précieuse dans les jeux, les énigmes et les problèmes à résoudre au quotidien ! Annonces sponsorisées Cet outil a été mis à jour, merci de signaler tout problème. Test de la Conjecture de Syracuse Conjecture de Syracuse Personnalisée Réponses aux Questions Comment calculer la conjecture de Syracuse ? At-on déjà trouvé un nombre qui n'obéi pas à la conjecture de Syracuse ? Non, personne n'a trouvé de nombre pour lequel ça ne fonctionne pas et personne n'a trouvé de preuve mathématique que la conjecture fonctionne toujours. On trouve les noms de : Conférences. Le cadran solaire équatorial et horizontal - La main à la pâte 22.
Principe cadran face été voir l’activité dans la rubrique Le ciel et la Terre Cette réalisation est proposée par le Comité de Liaison Enseignants Astronomes (académie de Nice) Réalisation dans un boitier de CD Rom Imprimer à l’échelle normale le document pdf ci-dessous.
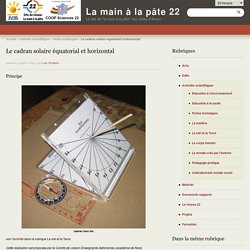
Découper chaque partie et les coller sur un bristol un peu plus épais. Marquer avec précision le point de perçage du boitier et faire un trou de 3mm avec une pointe en fer passée quelques minutes dans la flamme d’une bougie. Marquer le point inférieur sans traverser. Préparer le style (pique à brochette) et une paille plastique à la bonne longueur indiquée sur le document en fonction du lieu d’observation. Utilisation Placer le cadran sur un plan horizontal dans une zone bien dégagée. Avec une boussole, orienter le coté du boitier selon la ligne Nord-Sud Lire l’heure solaire en repérant la position de l’ombre portée sur la surface supérieure (en été), sous la face inférieure (en hiver), cadran face hiver cadran au sol.
Planétaire héliocentrique - La main à la pâte 22. Présentation planetaire Il s’agit de tracer sur un support carton de 30cmx30cm les trajectoires circulaires des planètes visibles à l’oeil nu : Vénus Mars Jupiter Saturne Il faudra aussi placer la Terre : ces planètes sont matérialisées par des épingles de couleur.
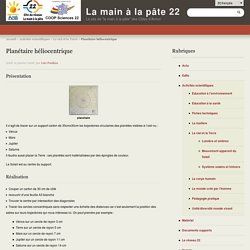
Le Soleil est au centre du support. Réalisation Couper un carton de 30 cm de côté recouvrir d’une feuille A3 blanche Trouver le centre par intersection des diagonales Tracer les cercles concentriques sans respecter une échelle des distances car c’est seulement la position des astres sur leurs trajectoires qui nous intéresse ici. L’échelle de l’Univers : de l’infiniment petit à l’infiniment grand. Si la Lune faisait juste un pixel - une carte à peu près à l'echelle. La Lune Io Europe Ganymède Callisto Titan Triton PlutonPlus d'info sur Pluton(on l'aime toujours même si elle ne fait plus partie des planètes) On vient de faire à peu près 10 millions de km.
C'est vide ici. Voici la première planète... Apparemment, les planètes sont assez éloignées. Nous allons bientôt arriver vers une nouvelle planète. L'Espace est composé de beaucoup d'espace. On est bientôt à la maison. Destination: Mars! Il faudrait environ sept mois pour parcourir cette distance avec un vaisseau spatial. Installez-vous confortablement et détendez-vous . On est bientôt arrivé? Sérieusement. Sur votre gauche, du noir. A 120km/h il faudrait 320 ans pour arriver ici en voiture depuis La Terre. Toutes ces distances ne sont que des moyennes. En fait, si vous prévoyez bien le coup, vous pouvez vous déplacer relativement rapidement d'une planète à une autre.
En approche de Jupiter. Désolé. Cette promenade nous laisse du temps pour penser...