

LEXIQUE de physique quantique. Théorie des quanta. Un article de Wikipédia, l'encyclopédie libre.
La théorie des quanta est le nom donné à une théorie physique qui tente de modéliser le comportement de l'énergie à très petite échelle à l'aide des quanta (pluriel du terme latin quantum), quantités discontinues. Son introduction a bousculé plusieurs idées reçues en physique de l'époque, au début du XXe siècle. Elle a servi de pont entre la physique classique et la physique quantique, dont la pierre angulaire, la mécanique quantique, est née en 1925. Elle a été initiée par Max Planck en 1900, puis développée essentiellement par Albert Einstein, Niels Bohr, Arnold Sommerfeld, Hendrik Anthony Kramers, Werner Heisenberg, Wolfgang Pauli et Louis de Broglie entre 1905 et 1924. Historique[modifier | modifier le code] La physique classique en vigueur à la fin du XIXe siècle comprenait les théories suivantes : Problèmes expérimentaux de la fin du XIXe siècle[modifier | modifier le code] Le rayonnement du corps noir[modifier | modifier le code] où.
Contrafactualité (physique) Un article de Wikipédia, l'encyclopédie libre.
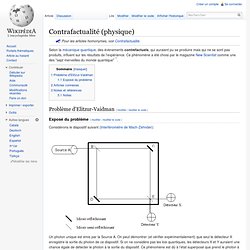
Selon la mécanique quantique, des évènements contrefactuels, qui auraient pu se produire mais qui ne se sont pas produits, influent sur les résultats de l'expérience. Ce phénomène a été choisi par le magazine New Scientist comme une des "sept merveilles du monde quantique" [1]. Considérons le dispositif suivant (Interféromètre de Mach-Zehnder): Un photon unique est émis par la Source A. On peut démontrer (et vérifier expérimentalement) que seul le détecteur X enregistre la sortie du photon de ce dispositif. Cette expérience est très semblable dans l’esprit à celle des fentes d'Young, mais permet de plus de mettre en évidence la contrafactualité des phénomènes quantiques : Modifions ce dispositif pour que C soit maintenant un détecteur de photon, du même type que X ou Y.
Soit le photon est détecté par C (probabilité ½)Soit les détecteurs X et Y ont une chance égale de détecter le photon (probabilité ¼ et ¼) État quantique. Un article de Wikipédia, l'encyclopédie libre.
L'état d'un système physique décrit tous les aspects de ce système, dans le but de prévoir les résultats des expériences que l'on peut réaliser. Case quantique. Un article de Wikipédia, l'encyclopédie libre.
En physique, en mécanique quantique, dans le modèle de Bohr, les cases quantiques sont les places dans les orbitales atomiques qui peuvent être occupées par un électron, ou par une paire d'électrons de spin complémentaires. Nombres quantiques[modifier | modifier le code] Le nuage électronique de chaque atome peut être défini par quatre nombres dits « quantiques », puisqu'ils ne prennent que certaines valeurs quantifiées : n : nombre quantique « principal » qui peut prendre toutes les valeurs entières égales ou supérieures à 1 soit 1, 2, 3, 4… Il définit en grande partie l'énergie de l'électron ainsi que la taille de l'orbitale qui augmente à mesure que n augmente.l : nombre quantique « secondaire » qui peut prendre toutes les valeurs entières comprises entre 0 et n-1.
Cela signifie par exemple, dans le cas où n = 2, que l peut être égal à 0 ou à 1. Par exemple : Intrication quantique. Un article de Wikipédia, l'encyclopédie libre.
Historique[modifier | modifier le code] Le caractère surprenant des états intriqués a pour la première fois été souligné par Einstein, Podolsky et Rosen dans un article de 1935 qui tentait de montrer que la mécanique quantique était incomplète. Dans cet article, les auteurs décrivent une expérience de pensée qui restera connue comme le paradoxe EPR. Principe de superposition quantique. Un article de Wikipédia, l'encyclopédie libre.
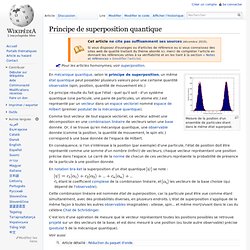
Mesure de la position d'un ensemble de particules étant dans le même état superposé. En mécanique quantique, selon le principe de superposition, un même état quantique peut posséder plusieurs valeurs pour une certaine quantité observable (spin, position, quantité de mouvement etc.) Ce principe résulte du fait que l'état - quel qu'il soit - d'un système quantique (une particule, une paire de particules, un atome etc.) est représenté par un vecteur dans un espace vectoriel nommé espace de Hilbert (premier postulat de la mécanique quantique). En notation bra-ket la superposition d'un état quantique se note : Théorie quantique des champs. Un article de Wikipédia, l'encyclopédie libre.
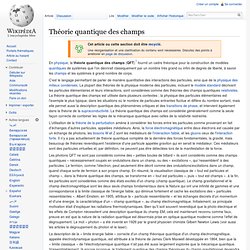
Les photons QFT ne sont pas considérés comme des « petites boules de billard » ils sont considérés comme des champs quantiques – nécessairement coupés en ondulations dans un champ, ou des « excitations », qui 'ressemblent' à des particules. Le fermion, comme l'électron, peut seulement être décrit comme des ondulations/excitations dans un champ, quand chaque sorte de fermion a son propre champ.
Dualité onde-particule. Un article de Wikipédia, l'encyclopédie libre.
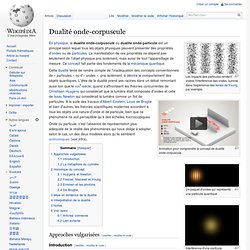
Les impacts des particules rendent visible l'interférence des ondes, comme dans l'expérience des fentes de Young, par exemple. Animation pour comprendre le concept de dualité onde-corpuscule Un paquet d'ondes qui représente une particule quantique Interférence d'une particule quantique avec elle-même Cette dualité tente de rendre compte de l'inadéquation des concepts conventionnels de « particules » ou d'« ondes », pris isolément, à décrire le comportement des objets quantiques.
Dualité onde corpuscule. Réduction du paquet d'onde. Un article de Wikipédia, l'encyclopédie libre.
La réduction du paquet d'onde est un concept de la mécanique quantique selon lequel, après une mesure, un système physique voit son état entièrement réduit à celui qui a été mesuré. Pendant longtemps, le processus par lequel cette réduction a lieu a été inconnu des physiciens, ce qui les a contraint à en faire un axiome de la théorie afin de rester conforme aux résultats expérimentaux. Le concept de réduction du paquet d'onde implique de nombreuses difficultés sur le plan logique et épistémologique. À ce titre, il a induit de nombreux et parfois célèbres débats au sein de la communauté scientifique. Instanton. Un article de Wikipédia, l'encyclopédie libre.
Les instantons ont été introduits par Gerard 't Hooft dans les années 1970. Definition[modifier | modifier le code] Instanton. Quantum theory[edit] they appear in the path integral as the leading quantum corrections to the classical behavior of a system, andthey can be used to study the tunneling behavior in various systems such as a Yang–Mills theory. Mathematics[edit] Yang–Mills instantons have been explicitly constructed in many cases by means of twistor theory, which relates them to algebraic vector bundles on algebraic surfaces, and via the ADHM construction, or hyperkähler reduction (see hyperkähler manifold), a sophisticated linear algebra procedure. The groundbreaking work of Simon Donaldson, for which he was later awarded the Fields medal, used the moduli space of instantons over a given four-dimensional differentiable manifold as a new invariant of the manifold that depends on its differentiable structure and applied it to the construction of homeomorphic but not diffeomorphic four-manifolds.
Many methods developed in studying instantons have also been applied to monopoles. Quantum mechanics[edit] Example. Soliton. Un article de Wikipédia, l'encyclopédie libre. Un soliton est une onde solitaire qui se propage sans se déformer dans un milieu non linéaire et dispersif. Intégrale de chemin. Un article de Wikipédia, l'encyclopédie libre. C'est Richard Feynman qui a introduit les intégrales de chemin en physique dans sa thèse, soutenue en mai 1942, portant sur la formulation de la mécanique quantique basée sur le lagrangien[2]. En raison de la seconde Guerre mondiale, ces résultats ne seront publiés qu'en 1948[3]. Cet outil mathématique s'est rapidement imposé en physique théorique avec sa généralisation à la théorie quantique des champs, permettant notamment une quantification des théories de jauge non-abéliennes plus simple que la procédure de quantification canonique.
Par ailleurs, le mathématicien Mark Kac a ensuite développé un concept similaire pour la description théorique du mouvement brownien, s'inspirant de résultats obtenus par Norbert Wiener dans les années 1920. On parle dans ce cas de la formule de Feynman-Kac, qui est une intégrale pour la mesure de Wiener[4]. Genèse du concept d'intégrale de chemin[modifier | modifier le code] On sait que : Feynman. — « Oui. » où.
Principe d'incertitude. Un article de Wikipédia, l'encyclopédie libre. Vues spatiale (position) et fréquentielle (impulsion) de (a) une onde, (b) un paquet d'onde et (c) un corpuscule. L'onde étant de fréquence pure, son impulsion est définie mais elle n'est pas localisée dans l'espace. Inversement, le corpuscule est localisé mais n'a pas de fréquence déterminée. Le cas général est celui du paquet d'onde qui est distribué en fréquence comme en espace. Du fait de la dualité entre les deux représentations l'étalement spatial est inversement proportionnel à l'étalement fréquentiel.
La fonction d'onde d'une particule initialement très localisée Le principe d'incertitude (ou principe d'indétermination) énonce que, pour une particule massive donnée, on ne peut pas connaître simultanément sa position et sa vitesse. Ce principe fut énoncé au printemps 1927 par Heisenberg lors des balbutiements de la mécanique quantique. Le terme « incertitude » est le terme historique pour ce principe. Paradoxe EPR. Un article de Wikipédia, l'encyclopédie libre. Pour les articles homonymes, voir EPR. Le paradoxe EPR, abréviation de Einstein-Podolsky-Rosen, est une expérience de pensée, élaborée par Albert Einstein, Boris Podolsky et Nathan Rosen, dont le but premier était de réfuter l'interprétation de Copenhague de la physique quantique. L'interprétation de Copenhague s'oppose à l'existence d'un quelconque état d'un système quantique avant toute mesure.
En effet, il n'existe pas de preuve que cet état existe avant son observation et le supposer amène à certaines contradictions. Ce paradoxe fut élaboré par Albert Einstein et deux de ses collaborateurs Boris Podolsky et Nathan Rosen pour soulever ce qui semblait apparaître comme une contradiction dans la mécanique quantique, ou du moins une contradiction avec au moins l'une des trois hypothèses suivantes : Nombre quantique. Un article de Wikipédia, l'encyclopédie libre. Un nombre quantique est, en mécanique quantique, un élément d'un jeu de nombres permettant de définir l'état quantique complet d'un système. Chaque nombre quantique définit la valeur d'une quantité conservée dans la dynamique d'un système quantique. En physique des particules, les nombres quantiques dits « intrinsèques » sont des caractéristiques de chaque type de particule élémentaire. Vide quantique.