

Limit Calculator - Symbolab. Srinivasa Ramanujan. Srinivasa Ramanujan Iyengar FRS (pronunciation: i/sriː.ni.vaː.sə raː.maː.nʊ.dʒən/) (22 December 1887 – 26 April 1920) was an Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series, and continued fractions.
Ramanujan initially developed his own mathematical research in isolation; it was quickly recognized by Indian mathematicians. When his skills became apparent to the wider mathematical community, centred in Europe at the time, he began a famous partnership with the English mathematician G. Srinivasa Ramanujan, a Mathematician Brilliant Beyond Comparison. Had he emerged in a city of advanced learning from a family of noted mathematicians his accomplishments would still have been stunning, but he was born into a poor family of no notable professional attainments in a part of the world where hardly anyone could understand even the nature of his talents.

The obstacles to his achieving his goal of becoming a professional mathematician were by reasonable assessment insurmountable. Yet he did, and people around the world still marvel at attainments of Srinavasa Ramanujan. Ramanujan was born on December 22, 1887 in Erode, a minor city in Madras State (now Tamil Nadu) in South India. His father was a clerk in a fabric store. The family was Brahmin and Ramanujan's maternal grandfather was a minor official in a local court. Triality. The automorphisms of the Dynkin diagram D4 give rise to triality in Spin(8).
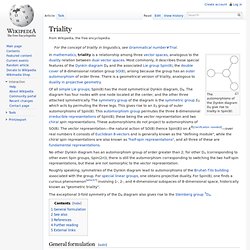
No other Dynkin diagram has an automorphism group of order greater than 2; for other Dn (corresponding to other even Spin groups, Spin(2n)), there is still the automorphism corresponding to switching the two half-spin representations, but these are not isomorphic to the vector representation. Roughly speaking, symmetries of the Dynkin diagram lead to automorphisms of the Bruhat–Tits building associated with the group.
For special linear groups, one obtains projective duality. For Spin(8), one finds a curious phenomenon[which?] Intuitionism. In the philosophy of mathematics, intuitionism, or neointuitionism (opposed to preintuitionism), is an approach where mathematics is considered to be purely the result of the constructive mental activity of humans.
That is, given a set of axioms, the only propositions that can exist are those that can be constructed, directly or indirectly, by these axioms. In other words, for any proposition only a constructive proof may be used to examine its validity. Proofs by contradiction and proofs by induction are rejected. Truth and proof[edit] To an intuitionist, the claim that an object with certain properties exists is a claim that an object with those properties can be constructed. Category theory. A category with objects X, Y, Z and morphisms f, g, g ∘ f, and three identity morphisms (not shown) 1X, 1Y and 1Z.
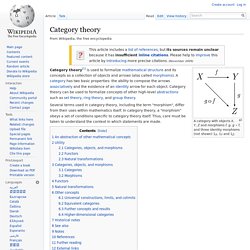
Several terms used in category theory, including the term "morphism", differ from their uses within mathematics itself. In category theory, a "morphism" obeys a set of conditions specific to category theory itself. Thus, care must be taken to understand the context in which statements are made. An abstraction of other mathematical concepts[edit] The most accessible example of a category is the category of sets, where the objects are sets and the arrows are functions from one set to another. Field (mathematics) Commutative rings ⊃ integral domains ⊃ integrally closed domains ⊃ unique factorization domains ⊃ principal ideal domains ⊃ Euclidean domains ⊃ fields ⊃ finite fields.
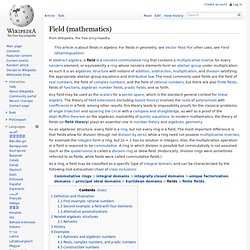
Intuitively, a field is a set F that is a commutative group with respect to two compatible operations, addition and multiplication, with "compatible" being formalized by distributivity, and the caveat that the additive identity (0) has no multiplicative inverse (one cannot divide by 0). Closure of F under addition and multiplication For all a, b in F, both a + b and a · b are in F (or more formally, + and · are binary operations on F).
Associativity of addition and multiplication For all a, b, and c in F, the following equalities hold: a + (b + c) = (a + b) + c and a · (b · c) = (a · b) · c.
Probability. Ramurile Matematicii « orademate. Millennium Prize Problems. The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000.
As of July 2013, six of the problems remain unsolved. A correct solution to any of the problems results in a US $1,000,000 prize (sometimes called a Millennium Prize) being awarded by the institute. The Poincaré conjecture was solved by Grigori Perelman, but he declined the award in 2010. Problems[edit] P versus NP[edit] Timeline of mathematics. A timeline of pure and applied mathematics history.

Timeline[edit] Rhetorical stage[edit] Before 1000 BC[edit] SUBIECTE MATEMATICĂ BAC 2013: iată subiectele şi baremul la matematică, toate profilurile.
Absolute Infinite. The Absolute Infinite is mathematician Georg Cantor's concept of an "infinity" that transcends the transfinite numbers.
Cantor linked the Absolute Infinite with God.[1] He held that the Absolute Infinite had various mathematical properties, including the reflection principle which says that every property of the Absolute Infinite is also held by some smaller object.[2] Cantor's view[edit] Cantor is quoted as saying: Transfinite number. Transfinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers, yet not necessarily absolutely infinite.
The term transfinite was coined by Georg Cantor, who wished to avoid some of the implications of the word infinite in connection with these objects, which were nevertheless not finite. Few contemporary writers share these qualms; it is now accepted usage to refer to transfinite cardinals and ordinals as "infinite". However, the term "transfinite" also remains in use. Definition[edit]
Inner product space. Geometric interpretation of the angle between two vectors defined using an inner product Definition[edit] Formally, an inner product space is a vector space V over the field F together with an inner product, i.e., with a map that satisfies the following three axioms for all vectors and all scalars. Algebraic geometry. Algebraic geometry is a branch of mathematics, classically studying zeros of polynomial equations. Modern algebraic geometry is based on more abstract techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. Algebraic geometry occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex analysis, topology and number theory. Initially a study of systems of polynomial equations in several variables, the subject of algebraic geometry starts where equation solving leaves off, and it becomes even more important to understand the intrinsic properties of the totality of solutions of a system of equations, than to find a specific solution; this leads into some of the deepest areas in all of mathematics, both conceptually and in terms of technique.
Sigma-algebra. If X = {a, b, c, d}, one possible σ-algebra on X is Σ = {∅, {a, b}, {c, d}, {a, b, c, d}}, where ∅ is the empty set. However, a finite algebra is always a σ-algebra. If {A1, A2, A3, …} is a countable partition of X then the collection of all unions of sets in the partition (including the empty set) is a σ-algebra. A more useful example is the set of subsets of the real line formed by starting with all open intervals and adding in all countable unions, countable intersections, and relative complements and continuing this process (by transfinite iteration through all countable ordinals) until the relevant closure properties are achieved (a construction known as the Borel hierarchy).
Motivation[edit] There are at least three key motivators for σ-algebras: defining measures, manipulating limits of sets, and managing partial information characterized by sets. Sample space. For example, if the experiment is tossing a coin, the sample space is typically the set {head, tail}. For tossing two coins, the corresponding sample space would be {(head,head), (head,tail), (tail,head), (tail,tail)}. For tossing a single six-sided die, the typical sample space is {1, 2, 3, 4, 5, 6} (in which the result of interest is the number of pips facing up).[2] Multiple sample spaces[edit] Equally likely outcomes[edit] Up or down?
List of mathematical symbols. When reading the list, it is important to recognize that a mathematical concept is independent of the symbol chosen to represent it. For many of the symbols below, the symbol is usually synonymous with the corresponding concept (ultimately an arbitrary choice made as a result of the cumulative history of mathematics), but in some situations a different convention may be used. For example, depending on context, the triple bar "≡" may represent congruence or a definition. Further, in mathematical logic, numerical equality is sometimes represented by "≡" instead of "=", with the latter representing equality of well-formed formulas. In short, convention dictates the meaning. Each symbol is shown both in HTML, whose display depends on the browser's access to an appropriate font installed on the particular device, and in TeX, as an image. Number sense. Graph theory. Tree (graph theory) Tree Visualization.
Phylogenetic tree. List of phylogenetic tree visualization software. Dendroscope. Archaeopteryx (evolutionary tree visualization and analysis) Tree editors.