

Multiverse. Existentialism. Existentialism is a term applied to the work of certain late 19th- and 20th-century philosophers who, despite profound doctrinal differences,[1][2][3] shared the belief that philosophical thinking begins with the human subject—not merely the thinking subject, but the acting, feeling, living human individual.[4] In existentialism, the individual's starting point is characterized by what has been called "the existential attitude", or a sense of disorientation and confusion in the face of an apparently meaningless or absurd world.[5] Many existentialists have also regarded traditional systematic or academic philosophies, in both style and content, as too abstract and remote from concrete human experience.[6][7] Definitional issues and background[edit] There has never been general agreement on the definition of existentialism.
The term is often seen as an historical convenience as it was first applied to many philosophers in hindsight, long after they had died. Concepts[edit] Existentialism. Existentialism is a term applied to the work of certain late 19th- and 20th-century philosophers who, despite profound doctrinal differences,[1][2][3] shared the belief that philosophical thinking begins with the human subject—not merely the thinking subject, but the acting, feeling, living human individual.[4] In existentialism, the individual's starting point is characterized by what has been called "the existential attitude", or a sense of disorientation and confusion in the face of an apparently meaningless or absurd world.[5] Many existentialists have also regarded traditional systematic or academic philosophies, in both style and content, as too abstract and remote from concrete human experience.[6][7] Definitional issues and background[edit] There has never been general agreement on the definition of existentialism.
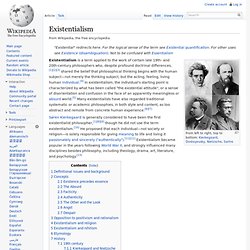
The term is often seen as a historical convenience as it was first applied to many philosophers in hindsight, long after they had died. Dimension (mathematics and physics) A diagram showing the first four spatial dimensions. 1-D: Two points A and B can be connected to a line, giving a new line segment AB. 2-D: Two parallel line segments AB and CD can be connected to become a square, with the corners marked as ABCD. 3-D: Two parallel squares ABCD and EFGH can be connected to become a cube, with the corners marked as ABCDEFGH. 4-D: Two parallel cubes ABCDEFGH and IJKLMNOP can be connected to become a hypercube, with the corners marked as ABCDEFGHIJKLMNOP.
In physical terms, dimension refers to the constituent structure of all space (cf. volume) and its position in time (perceived as a scalar dimension along the t-axis), as well as the spatial constitution of objects within—structures that correlate with both particle and field conceptions, interact according to relative properties of mass—and are fundamentally mathematical in description. The concept of dimension is not restricted to physical objects. Number. A notational symbol that represents a number is called a numeral.
In addition to their use in counting and measuring, numerals are often used for labels (telephone numbers), for ordering (serial numbers), and for codes (e.g., ISBNs). Ontic. In philosophy, ontic (from the Greek ὄν, genitive ὄντος: "of that which is") is physical, real, or factual existence.
"Ontic" describes what is there, as opposed to the nature or properties of that being. To illustrate: Bootstrap paradox. The Unreality of Time. The A-series[edit] "...the series of positions running from the far past through the near past to the present, and then from the present to the near future and the far future...
" McTaggart says, "the distinctions of past, present, and future are essential to time and... if the distinctions are never true of reality, then no reality is in time. " He considers the A-series to be temporal, a true time series because it embodies these distinctions and embodies change. Novikov self-consistency principle. The Novikov self-consistency principle, also known as the Novikov self-consistency conjecture, is a principle developed by Russian physicist Igor Dmitriyevich Novikov in the mid-1980s to solve the problem of paradoxes in time travel, which is theoretically permitted in certain solutions of general relativity (solutions containing what are known as closed timelike curves).
The principle asserts that if an event exists that would give rise to a paradox, or to any "change" to the past whatsoever, then the probability of that event is zero. It would thus be impossible to create time paradoxes. History of the principle[edit] Physicists have long been aware that there are solutions to the theory of general relativity which contain closed timelike curves, or CTCs—see for example the Gödel metric. Self-fulfilling prophecy.
A self-fulfilling prophecy is a prediction that directly or indirectly causes itself to become true, by the very terms of the prophecy itself, due to positive feedback between belief and behavior.
Although examples of such prophecies can be found in literature as far back as ancient Greece and ancient India, it is 20th-century sociologist Robert K. Merton who is credited with coining the expression "self-fulfilling prophecy" and formalizing its structure and consequences. List of paradoxes.
This is a list of paradoxes, grouped thematically.
The grouping is approximate, as paradoxes may fit into more than one category. Because of varying definitions of the term paradox, some of the following are not considered to be paradoxes by everyone. This list collects only scenarios that have been called a paradox by at least one source and have their own article. Although considered paradoxes, some of these are based on fallacious reasoning, or incomplete/faulty analysis. Informally, the term is often used to describe a counter-intuitive result. Logic[edit] Self-reference[edit] These paradoxes have in common a contradiction arising from self-reference.
Barber paradox: A barber (who is a man) shaves all and only those men who do not shave themselves. Tautology (logic) Is sometimes used to denote an arbitrary tautology, with the dual symbol (falsum) representing an arbitrary contradiction.
Tautologies are a key concept in propositional logic, where a tautology is defined as a propositional formula that is true under any possible Boolean valuation of its propositional variables. Naive set theory. Russell's paradox. In the foundations of mathematics, Russell's paradox (also known as Russell's antinomy), discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction.
The same paradox had been discovered a year before by Ernst Zermelo but he did not publish the idea, which remained known only to Hilbert, Husserl and other members of the University of Göttingen. In 1908, two ways of avoiding the paradox were proposed, Russell's type theory and the Zermelo set theory, the first constructed axiomatic set theory. Zermelo's axioms went well beyond Frege's axioms of extensionality and unlimited set abstraction, and evolved into the now-canonical Zermelo–Fraenkel set theory (ZF).[1] Informal presentation[edit] Ludwig Wittgenstein. Noam Chomsky. Avram Noam Chomsky (/ˈnoʊm ˈtʃɒmski/; born December 7, 1928) is an American linguist, philosopher,[21][22] cognitive scientist, logician,[23][24][25] political commentator and anarcho-syndicalist activist.
Sometimes described as the "father of modern linguistics",[26][27] Chomsky is also a major figure in analytic philosophy.[21] He has spent most of his career at the Massachusetts Institute of Technology (MIT), where he is currently Professor Emeritus, and has authored over 100 books. He has been described as a prominent cultural figure, and was voted the "world's top public intellectual" in a 2005 poll.[28] Born to a middle-class Ashkenazi Jewish family in Philadelphia, Chomsky developed an early interest in anarchism from relatives in New York City. He later undertook studies in linguistics at the University of Pennsylvania, where he obtained his BA, MA, and PhD, while from 1951 to 1955 he was appointed to Harvard University's Society of Fellows. Early life Childhood: 1928–45. Rudolf Carnap. Rudolf Carnap (May 18, 1891 – September 14, 1970) was a German-born philosopher who was active in Europe before 1935 and in the United States thereafter.
He was a major member of the Vienna Circle and an advocate of logical positivism. Life and work[edit] Carnap's Birthplace in Wuppertal.