Multiset. Overview[edit] History[edit] Blizard (1989) traced multisets back to the very origin of numbers, arguing that “in ancient times, the number n was often represented by a collection of n strokes, tally marks, or units.” These and similar collections of objects are multisets as strokes, tally marks, or units are considered indistinguishable. This shows that people implicitly used multisets even before mathematics emerged. This shows that necessity in this structure has been always so urgent that multisets have been several times rediscovered and appeared in literature under different names (Blizard, 1991).
For instance, they are called bags by Peterson (1981), who attributed this term to Cerf, Gostelow, Estrin, and Volanski (1971). Although multisets were implicitly utilized from ancient times, their explicit exploration happened much later. In the explicit form, multisets appeared in the work of Richard Dedekind "Was sind und was sollen die Zahlen? " Formal definition[edit] where to the set in. Fuzzy set. It has been suggested by Thayer Watkins that Zadeh's ethnicity is an example of a fuzzy set because "His father was Turkish-Iranian (Azerbaijani) and his mother was Russian. His father was a journalist working in Baku, Azerbaijan in the Soviet Union...Lotfi was born in Baku in 1921 and lived there until his family moved to Tehran in 1931.
"[5] Definition[edit] A fuzzy set is a pair where is a set and For each the value is called the grade of membership of in For a finite set the fuzzy set is often denoted by Let Then is called not included in the fuzzy set if is called fully included if , and is called a fuzzy member if .[6] The set is called the support of and the set is called its kernel. Is called the membership function of the fuzzy set of a given kind; usually it is required that Fuzzy logic[edit] As an extension of the case of multi-valued logic, valuations ( ) of propositional variables ( ) into a set of membership degrees ( Fuzzy number[edit] A fuzzy number is a convex, normalized fuzzy set .
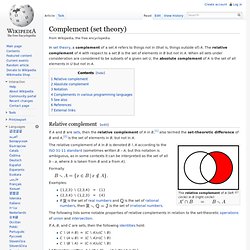
Entropy[edit] Complement (set theory) In set theory, a complement of a set A refers to things not in (that is, things outside of) A. The relative complement of A with respect to a set B is the set of elements in B but not in A. When all sets under consideration are considered to be subsets of a given set U, the absolute complement of A is the set of all elements in U but not in A. The relative complement of A (left circle) in B (right circle): The relative complement of A in B is denoted B ∖ A according to the ISO 31-11 standard (sometimes written B – A, but this notation is ambiguous, as in some contexts it can be interpreted as the set of all b – a, where b is taken from B and a from A).
Formally Examples: {1,2,3} ∖ {2,3,4} = {1}{2,3,4} ∖ {1,2,3} = {4}If is the set of real numbers and is the set of rational numbers, then is the set of irrational numbers. [ Alternately written: A ∖ (B ∖ C) = (A ∖ B)∪(A ∩ C) ] The absolute complement of A in U: or if U is fixed, that is: Ac = U ∖ A. De Morgan's laws:[1] Complement laws:[1] Clojure. Venn diagram. Example[edit] Sets A (creatures with two legs) and B (creatures that can fly) Humans and penguins are bipedal, and so are then in the orange circle, but since they cannot fly they appear in the left part of the orange circle, where it does not overlap with the blue circle.
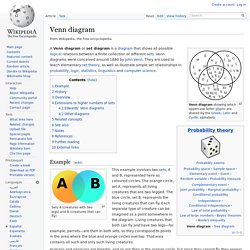
Mosquitoes have six legs, and fly, so the point for mosquitoes is in the part of the blue circle that does not overlap with the orange one. Creatures that are not two-legged and cannot fly (for example, whales and spiders) would all be represented by points outside both circles. History[edit] Venn diagrams were introduced in 1880 by John Venn (1834–1923) in a paper entitled On the Diagrammatic and Mechanical Representation of Propositions and Reasonings in the "Philosophical Magazine and Journal of Science", about the different ways to represent propositions by diagrams.[1][2] The use of these types of diagrams in formal logic, according to Ruskey and M. In the 20th century, Venn diagrams were further developed. A. Euler diagram. An Euler diagram illustrating that the set of "animals with four legs" is a subset of "animals", but the set of "minerals" is disjoint (has no members in common) with "animals" Venn and Euler diagrams were incorporated as part of instruction in set theory as part of the new math movement in the 1960s.
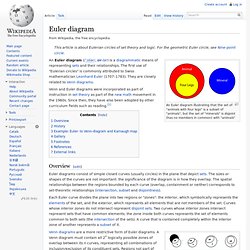
Since then, they have also been adopted by other curriculum fields such as reading.[1] Overview[edit] Examples of small Venn diagrams(on left) with shaded regions representing empty sets, showing how they can be easily transformed into equivalent Euler diagrams (right). Venn diagrams are a more restrictive form of Euler diagrams. In a logical setting, one can use model theoretic semantics to interpret Euler diagrams, within a universe of discourse. Often a set of well-formedness conditions are imposed; these are topological or geometric constraints imposed on the structure of the diagram. History[edit] Photo of page from Hamilton's 1860 "Lectures" page 180. And the proposed deduction is: Set theory. The modern study of set theory was initiated by Georg Cantor and Richard Dedekind in the 1870s. 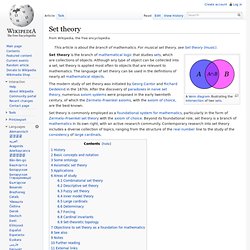After the discovery of paradoxes in naive set theory, numerous axiom systems were proposed in the early twentieth century, of which the Zermelo–Fraenkel axioms, with the axiom of choice, are the best-known.
Set theory is commonly employed as a foundational system for mathematics, particularly in the form of Zermelo–Fraenkel set theory with the axiom of choice. Beyond its foundational role, set theory is a branch of mathematics in its own right, with an active research community. Contemporary research into set theory includes a diverse collection of topics, ranging from the structure of the real number line to the study of the consistency of large cardinals. History[edit] Georg Cantor Mathematical topics typically emerge and evolve through interactions among many researchers.
Cantor's work initially polarized the mathematicians of his day. Basic concepts and notation[edit] Some ontology[edit] Naive set theory.