

Paul Nylander. List of nonlinear partial differential equations. In mathematics and physics, nonlinear partial differential equations are (as their name suggests) partial differential equations with nonlinear terms.
They describe many different physical systems, ranging from gravitation to fluid dynamics, and have been used in mathematics to solve problems such as the Poincaré conjecture and the Calabi conjecture . They are difficult to study: there are almost no general techniques that work for all such equations, and usually each individual equation has to be studied as a separate problem. Vlasov equation. The Vlasov equation is a differential equation describing time evolution of the distribution function of plasma consisting of charged particles with long-range (for example, Coulomb ) interaction.
The equation was first suggested for description of plasma by Anatoly Vlasov in 1938 [ 1 ] (see also [ 2 ] ) and later discussed by him in detail in a monograph. [ 3 ] Difficulties of the standard kinetic approach [ edit ] First, Vlasov argues that the standard kinetic approach based on the Boltzmann equation has difficulties when applied to a description of the plasma with long-range Coulomb interaction . He mentions the following problems arising when applying the kinetic theory based on pair collisions to plasma dynamics: Theory of pair collisions disagrees with the discovery by Rayleigh , Irving Langmuir and Lewi Tonks of natural vibrations in electron plasma.
Vlasov suggests that these difficulties originate from the long-range character of Coulomb interaction. Explicitly a PDE : and at time. Power flow study. In power engineering , the power flow study , also known as load-flow study , is an important tool involving numerical analysis applied to a power system.
A power flow study usually uses simplified notation such as a one-line diagram and per-unit system , and focuses on various forms of AC power (i.e.: voltages, voltage angles, real power and reactive power). It analyzes the power systems in normal steady-state operation. A number of software implementations of power flow studies exist. In addition to a power flow study, sometimes called the base case , many software implementations perform other types of analysis, such as short-circuit fault analysis, stability studies (transient & steady-state), unit commitment and economic load dispatch analysis.
In particular, some programs use linear programming to find the optimal power flow , the conditions which give the lowest cost per kilowatthour delivered. Van der Pol oscillator. Evolution of the limit cycle in the phase plane.
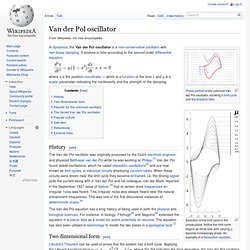
Notice the limit cycle begins as circle and, with varying μ, become increasingly sharp. An example of a Relaxation oscillator. In dynamics, the Van der Pol oscillator is a non-conservative oscillator with non-linear damping. Richards equation. The Richards equation represents the movement of water in unsaturated soils, and was formulated by Lorenzo A.
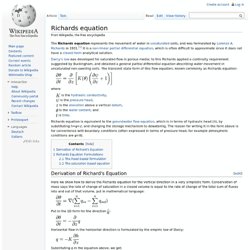
Richards in 1931. [ 1 ] It is a non-linear partial differential equation , which is often difficult to approximate since it does not have a closed-form analytical solution. Darcy's law was developed for saturated flow in porous media; to this Richards applied a continuity requirement suggested by Buckingham, and obtained a general partial differential equation describing water movement in unsaturated non-swelling soils . Nonlinear Schrödinger equation. In theoretical physics , the nonlinear Schrödinger equation ( NLS ) is a nonlinear variation of the Schrödinger equation .
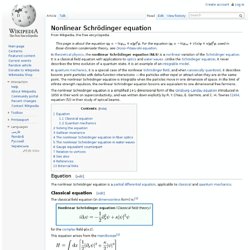
It is a classical field equation with applications to optics and water waves . Unlike the Schrödinger equation , it never describes the time evolution of a quantum state. It is an example of an integrable model . In quantum mechanics , it is a special case of the nonlinear Schrödinger field , and when canonically quantized , it describes bosonic point particles with delta-function interactions — the particles either repel or attract when they are at the same point. Nonlinear optics. Nonlinear optics remained unexplored until the discovery of Second harmonic generation shortly after demonstration of the first laser.
(Peter Franken et al. at University of Michigan in 1961) Navier–Stokes equations. The Navier–Stokes equations are also of great interest in a purely mathematical sense.
Somewhat surprisingly, given their wide range of practical uses, it has not yet been proven that in three dimensions solutions always exist (existence), or that if they do exist, then they do not contain any singularity. (They are smooth.) These are called the Navier–Stokes existence and smoothness problems. Boltzmann equation. In physics , specifically non-equilibrium statistical mechanics , the Boltzmann equation or Boltzmann transport equation describes the statistical behaviour of a fluid not in thermodynamic equilibrium , i.e. when there are temperature gradients in space causing heat to flow from hotter regions to colder ones, by the random (and biased) transport of particles .

It was devised by Ludwig Boltzmann in 1872. [ 1 ] The equation arises not by statistical analysis of all the individual positions and momenta of each particle in the fluid; rather by considering the probability that a number of particles all occupy a very small region of space (mathematically written d 3 r , where d means " differential ", a very small change) centered at the tip of the position vector r , and have very nearly equal small changes in momenta from a momentum vector p , at an instant of time. [ edit ] Overview [ edit ] The phase space and density function which is a 6-fold integral. . [ edit ] Principal statement and. Nonlinear system. Typically, the behavior of a nonlinear system is described by a nonlinear system of equations.
Nonlinear problems are of interest to engineers, physicists and mathematicians and many other scientists because most systems are inherently nonlinear in nature. As nonlinear equations are difficult to solve, nonlinear systems are commonly approximated by linear equations (linearization). This works well up to some accuracy and some range for the input values, but some interesting phenomena such as chaos[1] and singularities are hidden by linearization. It follows that some aspects of the behavior of a nonlinear system appear commonly to be chaotic, unpredictable or counterintuitive. Although such chaotic behavior may resemble random behavior, it is absolutely not random. For example, some aspects of the weather are seen to be chaotic, where simple changes in one part of the system produce complex effects throughout.