

Éval 211 sujet 1. Corrigé sujet 1 .pdf. Éval 211 sujet 2. Corrigé sujet 2. Cours nombres et calculs. Cours nombres et calculs. CORRIGE cours nombres et calculs. Approx racine de 2. Algo somme suite arithmétique. Approximation valeur absolue. Programme syracuse. Le nombre d'or. (Vitruve, architecte romain 1er siècle avant notre ère). Le nombre d'or. Fruits d'Eucalyptus provenant de Galice en Espagne.

On trouve des pentagones réguliers, mais aussi des carrés er des triangles équilatéraux. Lien avec l'ensoleillement Cela vient de ce que l'ensoleillement doit être maximum pour toutes les feuilles et on démontre que l'angle de deux feuilles consécutives doit être voisin d'un certain k ème de tour ; les fractions de Fibonacci sont les fractions les plus voisines de k. Les graines dans une fleur de tournesol Ammonite L'enroulement régulier d'une ammonite se fait suivant une spirale logarithmique. La découverte des quasicristaux, de molécules en forme de dodécaèdre (constitué de 12 pentagones), de certains virus ayant cette forme montre que la symétrie d'ordre cinq est assez fréquente dans la nature. " On doit être chez Fibonacci ! Voir aussi les liens externes suivants : géométrie dans la nature et aussi une vidéo splendide La nature par les nombres Un Aloés : Aloe polyphylla, Ils sont fous, ces nombres ! - Classification.
Pour qui s'ennuie en cours de maths - le ruban de Möbius - LMB #16. Infini histoire. Quand est apparue la notion d'infini?

À quel âge un enfant peut-il apprécier cette notion? Et, à l'origine des temps? Très difficile à s'imposer dans l'histoire, cette notion renvoyait à Dieu Tout-Puissant. Le monde fini a été créé pour l'homme. Les Grecs Ve siècle av. La chute d'eau d'Escher : le mouvement perpétuel en vidéo ! Je voulais évoquer dans cet article les liens entre les dessins d'Escher, la cristallographie et la topologie mais je suis tombé sur une vidéo plutôt bien faite qui m'a détourné de l'objectif initial.
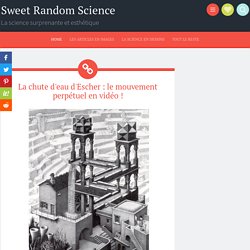
Je garde donc en réserve les vecteurs, les symétries, les atomes et les pavages de Penrose pour la prochaine fois ! La chute d'eau d'Escher Vous connaissez très probablement ce dessin où le graveur néerlandais, obsédé par les figures géométriques, les déformations et les boucles infinies, joue avec la perspective pour créer un cours d'eau perpétuel. Voici sa reproduction en "vrai", je vous laisse vous torturer les méninges pour comprendre le truc. Indice: pas de système de pompe, tout n'est qu'illusion. 1 Googol est très grand nombre à l'origine du nom google. Un article de Wikipédia, l'encyclopédie libre.
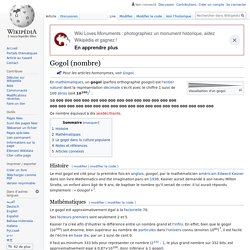
Pour les articles homonymes, voir Gogol. KEZAKO: Comment a-t-on découvert le nombre Pi? Images des mathématiques. Vous avez sans doute entendu parler du nombre qui intervient dans les formules que l’on apprenait à l’école élémentaire : pour le périmètre du cercle de rayon et pour l’aire délimitée par ce cercle (actuellement cela s’apprend en CM2 pour le périmètre et en 6ième pour l’aire).
Je me souviens aussi des valeurs approchées ( ou ou ) de ce nombre que j’ai apprises au CM1 au cours d’une leçon qui m’a marqué pour la vie. Notre instituteur nous apprit ainsi que le nombre permet de calculer le périmètre de tous les cercles, quel que soit leur rayon, et aussi l’aire des disques qu’ils délimitent. Le plus impressionnant pour moi fut d’apprendre que ce nombre a une infinité de décimales et que personne ne peut en donner la liste ni la décrire. Le nombre a une infinité de décimales et ce sont toutes des 3 ; la suite des décimales du nombre est facile à décrire : à partir de la cinquième décimale on juxtapose des blocs identiques .
Naissance des mathématiques européennes : la Grèce Vers 600 av. Le nombre pi. Pi Qui a inventé la notation La notation est due à Adrien Romain , au XVIe siècle .

Il a choisi car c’est la première lettre du mot grec « » ( se lit « peripheria ») qui signifie circonférence . Qui a calculé les décimales de. Tout est dans Pi ! Certains nombres sont beaucoup plus riches que d’autres.
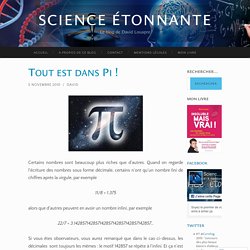
Quand on regarde l’écriture des nombres sous forme décimale, certains n’ont qu’un nombre fini de chiffres après la virgule, par exemple alors que d’autres peuvent en avoir un nombre infini, par exemple Si vous êtes observateurs, vous aurez remarqué que dans le cas ci-dessus, les décimales sont toujours les mêmes : le motif 142857 se répète à l’infini. Et ça n’est pas une exception puisqu’en fait tout nombre rationnel (c’est-à-dire tout nombre qui s’écrit comme une fraction) possède un développement décimal périodique. Pourquoi π est-il si fou ? Relativité 1. L'équation x²=2 n'est pas résoluble - Micmaths. Racine de deux. Pythagore et les pythagoriciens. Philosophe et mathématicien grec responsable d'importants développements en mathématiques, astronomie et musique Vie peu connue: figure mythique.

Œuvres connues que de façon indirecte. Root 2 and the deadly Marching Squares. Démonstration : 0,99999... = 1. La disparition de Perec. p28. Début d'année.