

Les Mathématiques : un jeu d'enfants - 1961 ONF/NFB. Arithmétique et calcul - Inria. Entiers naturels. Dans les chapitres précédents, nous avons déjà fait un large usage des symboles ℕ, ℤ, ℚ, ℝ, ℂ, pour désigner les ensembles de nombres couramment utilisés dans l'enseignement secondaire.
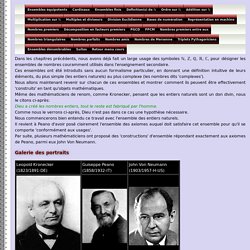
Ces ensembles ont été introduits sans aucun formalisme particulier, en donnant une définition intuitive de leurs éléments, du plus simple (les entiers naturels) au plus complexe (les nombres dits 'complexes'). Nous allons maintenant revenir sur chacun de ces ensembles et montrer comment ils peuvent être effectivement 'construits' en tant qu'objets mathématiques. Même des mathématiciens de renom, comme Kronecker, pensent que les entiers naturels sont un don divin, nous le citons ci-après: Dieu a créé les nombres entiers, tout le reste est fabriqué par l'homme.
Comme nous le verrons ci-après, Dieu n'est pas dans ce cas une hypothèse nécessaire. Nous commencerons bien entendu ce travail avec l'ensemble des entiers naturels. Interview : comprendre la théorie des nombres. Qu'est-ce qu'un Nombre ? - Hors-Série. Classification des nombres. Nombre cardinal. En linguistique, les nombres entiers naturels zéro, un, deux, trois, etc. s’appellent des adjectifs numéraux cardinaux.
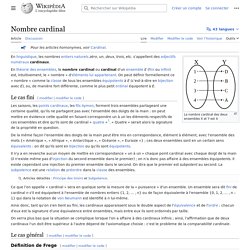
Le cas fini[modifier | modifier le code] De la même façon l'ensemble des doigts de la main peut être mis en correspondance, élément à élément, avec l'ensemble des mots {« Amérique », « Afrique », « Antarctique », « Océanie », « Eurasie »} ; ces deux ensembles sont en un certain sens équivalents : on dit qu'ils sont en bijection ou qu'ils sont équipotents. Ce que l'on appelle « cardinal » sera en quelque sorte la mesure de la « puissance » d'un ensemble. Un ensemble sera dit fini de cardinal n s'il est équipotent à l'ensemble de nombres entiers {1, 2, … , n} ou de façon équivalente à l'ensemble {0, 1, 2, … , n – 1} qui dans la notation de von Neumann est identifié à n lui-même. Nombre ordinal.
Spirale représentant les nombres ordinaux inférieurs à ωω.
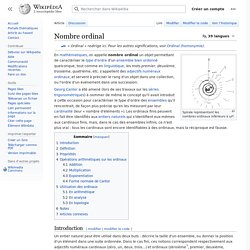
En mathématiques, on appelle nombre ordinal un objet permettant de caractériser le type d'ordre d'un ensemble bien ordonné quelconque, tout comme en linguistique, les mots premier, deuxième, troisième, quatrième, etc. s'appellent des adjectifs numéraux ordinaux, et servent à préciser le rang d'un objet dans une collection, ou l'ordre d'un événement dans une succession. Introduction[modifier | modifier le code] Un entier naturel peut être utilisé dans deux buts : décrire la taille d'un ensemble, ou donner la position d'un élément dans une suite ordonnée. Peut-on choisir les règles du calcul ? Ce texte se veut une introduction grand public aux problèmes mathématiques sur lesquels j'ai travaillé durant ma thèse : les groupes aléatoires.

Il a été conçu comme un exposé à donner au Palais de la Découverte. Introduction. 2.1. 6e-Division par zéro. Dictionnaire de base du vocabulaire des mathématiques A. Apex: sommet de certains solides; ex: l'apex du cône, de la pyramide, du prisme; la face opposée à l'apex est la base du solide Note: en anglais apex veut dire sommet, pluriel apexes ou apices Apollonien (remplissage -): avec des disques, les plus gros sont en contact.

Les vides sont remplis avec des disques plus petits, mais les plus grands possible (Illustration). Voir Fractales Apothème (un): en 2D, segment perpendiculaire à un côté d'un polygone et passant par son centre; distance du centre d'un polygone régulier à l'un de ses côtés. Appartenance: signifie l'élément a appartient à l'ensemble E; signifie a n'appartient pas à E – v. Dictionnaire des nombres - Contenu, pi, premier, parfait, or, magique.
Théorie des nombres. Théorie probabiliste des nombres. La théorie probabiliste des nombres est une branche de la théorie des nombres qui utilise explicitement les probabilités.Nous allons voir qu'il est parfois utile d'utiliser les probabilités pour répondre à certaines questions difficiles, même quand celles-ci portent sur les entiers naturels.
Nous allons nous intéresser à deux théorèmes principaux de cette théorie, dont les fondateurs sont Paul Erdös et Mark Kac : le théorème de Hardy-Ramanujan de 1917 etle théorème de Erdös-Kac de 1939. D'après le théorème fondamental de l'arithmétique, tout entier strictement positif peut être écrit comme un produit de nombres premiers d'une unique façon, à l'ordre près des facteurs. Livres d'Arithmétique et de Théorie des nombres.
Nombre algébrique. Un article de Wikipédia, l'encyclopédie libre.
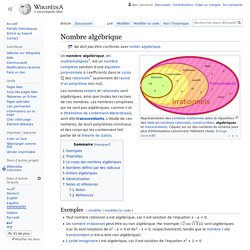
Un nombre algébrique, en mathématiques[a], est un nombre complexe solution d'une équation polynomiale à coefficients dans le corps. Nombre transcendant. Arithm'Antique n°36 - La moyenne, quelle moyenne ? Histoire arithmetique. Numbers. Mathématiques africaines. Mathématiques arabes. Tablettes babyloniennes. Mathématiques Chinoises.
Mathématiques égyptiennes. Maths grecques et latines. Chez les Incas, Mayas, Aztèques... Mathématiques indiennes. Mathématiques Russes.
Arithmétique. Théorie des nombres. Théorème des Restes Chinois - Calculatrice en Ligne. Rechercher un outil Restes Chinois Outil pour appliquer le théorème des restes chinois.

Le théorème des restes chinois permet de résoudre des systèmes d'équations de congruences en arithmétique modulaire. Résultats. PROMENADE MATHÉMATIQUE EN MÉSOPOTAMIE. Les préparatifs L’histoire du nombre commence il y a près de 4 000 ans, et chacun sait aujourd’hui, s’il a plus d’une douzaine d’années, qu’une valeur approchée est , et que ce nombre est utile pour calculer le périmètre ou l’aire d’un disque de rayon (ou de diamètre ) : Certains se souviennent aussi que la fraction est une excellente approximation.
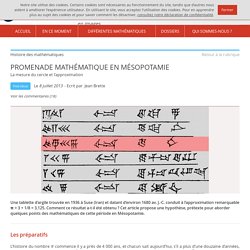
Elle est due à Archimède (287-212 av. J. 01 arithmetique introduction 01. Comment multiplier sans connaître ses tables? Dans la majorité des écoles d’Europe ou d’Amérique, par exemple, on apprend aux enfants à multiplier en apprenant par cœur les fameuses (et terribles...) « tables de multiplication » (pour en savoir plus sur ce sujet, nous renvoyons à cet excellent article d’Étienne Ghys).
Combien de fois les a-t-on récitées à nos parents, nos professeurs ? Combien d’enfants ont commencé à penser dès cet instant que pour « faire des maths », il fallait indéniablement apprendre plein de choses par cœur ? « Faire des maths » ce n’est pas apprendre plein de formules ou symboles étranges : c’est plutôt essayer de comprendre comment résoudre des problèmes le plus simplement possible. Néanmoins, nos méthodes éducatives ne permettent pas vraiment à nos enfants (ni à ceux des autres) de saisir cette beauté et cette subtilité qu’ont les mathématiques, et cela commence dès l’apprentissage de ces « terrifiantes » tables de multiplication [1].. Les calculs du citoyen Haros. Parmi ces ouvrages pédagogiques, l'un a connu plusieurs rééditions: Introduction abrégée sur les nouvelles mesures qui doivent être introduites dans toute la République au 1er vendémiaire an 10, avec des tables de rapports et de réductions, par C.H.
Haros. Cet ouvrage, originellement publié en l'an IX (1801) chez Firmin Didot, est en quelque sorte reconnu d'utilité publique par l'académie des sciences qui en publie un rapport élogieux. Par exemple, les académiciens Adrien-Marie Legendre et Gaspard Prony, terminent leur rapport sur l'ouvrage (lors de la séance du 21 ventôse an IX) avec le constat suivant: "le citoyen Haros est un des géomètres de la section des calculateurs du Bureau du Cadastre, où il a donné des preuves soutenues de science et de talent.
Les commissaires pensent que l'ouvrage de ce citoyen dont ils viennent de rendre compte à la classe, peut-être fort utile pour propager la connoissance du nouveau système des poids et mesure, et en faciliter l'usage". FrenicleGilain. Crypto18 12 2012handout. L'Encyclopédie en ligne des suites de nombres entiers. Les pages suivantes sont toutes en anglais Pour plus d'information sur l'Encyclopédie allez sur la page d'accueil Languages: English Shqip العربية Bangla Български Català 中文 (正體字, 简化字 (1), 简化字 (2)) Hrvatski Čeština Dansk Nederlands Esperanto Eesti فارسی Suomi Français Deutsch Ελληνικά ગુજરાતી עברית हिंदी Magyar Igbo Bahasa Indonesia Italiano 日本語 ಕನ್ನಡ 한국어 Lietuvių मराठी Bokmål Nynorsk Polski Português Română Русский Српски Slovenščina Español Svenska Tagalog ภาษาไทย Türkçe Українська اردو Tiếng Việt Cymraeg.
Journal de Théorie des Nombres de Bordeaux. Multiplication. L'équation x²=2 n'est pas résoluble - Micmaths. Racine de 2 CNRS image des maths. Appli identité remarquables Sophie Germain. Extraire racine. Dénombrement. Math Wonders to Inspire Teachers and Students. CD Calcul mental Lycee. La multiplication réinventée. Deux chercheurs ont développé une nouvelle méthode pour multiplier les très grands nombres. Une avancée potentiellement historique pour l’informatique. Cet article fait partie du TOP 5 des contenus les plus lus sur notre site en 2019 Adaptation des proportions d’une recette, calcul de pourcentages, résolution de problèmes de mathématiques, programmes informatiques… La multiplication est cruciale dans bien des domaines.
Rien d’étonnant donc à ce qu’elle soit l’une des quatre opérations algébriques rudimentaires enseignées à l’école – avec l’addition, la soustraction et la division. Or voilà que lors de travaux récents, Joris van der Hoeven, du Laboratoire d’informatique de l’École polytechnique1, à Palaiseau (Essonne), et son collègue australien David Harvey, de l’Université de Nouvelle-Galles du Sud, sont parvenus à développer une méthode permettant de multiplier plus rapidement les nombres entiers (donc sans virgule). L’incroyable lenteur de la méthode classique Un algorithme inédit C. CalculformelGazette. Théorie des nombres : combien d’indices remplacent une preuve ? Quatre chercheurs ont récemment mis au point un modèle qui remet en question une idée reçue dans leur domaine. Sur la foi de données obtenues par un calcul informatique, ils suggèrent que l'opinion dominante depuis des décennies sur un concept majeur est erronée. Théorème des restes chinois.
Séminaire Delange-Pisot-Poitou. Théorie des nombres. TheseGauthier. Bergeron Nicolas "Les "invariants arithmétiques" de H. Poincaré" Vincent Mineo-Kleiner - Jongler avec les nombres. Conséquences algébriques, appartenance aux idéaux et bases de Gröbner. La théorie de Galois et l’arithmétique Lafforgue. Géométrie et nombres. Gamma Function with Integer n. Gamma(n)=(n-1)! MarcDeleglise:MarcDeleglise. Soit θ et ψ les fonctions de Chebychev définies par θ(x)= Σp ≤ x log p et ψ(x) = Σpn ≤ x log p. La métode évidente de calcul de theta(x), énumerer les nombres premiers ≤ x en additionnant leurs logarithmes est de coût proportionnel à x log(log x). La différence psi(x) - theta(x) = Σp^n ≤ x, 2 ≤ n, est une somme ne portant que sur les nombres premiers inférieurs à x^(1/2) par la méthode naïve elle se calcule en temps O(x^(1/2 + eps)) pour tout eps > 0.
En utilisant alors l'algorithme de calcul de psi(x) en temps inférieur à O(x^(2/3 + eps) pour tout eps > 0, présenté dans M. Deléglise and J. Théorie des nombres et applications (en anglais) nicolas60. From Wolfram MathWorld. An abundant number, sometimes also called an excessive number, is a positive integer. From Wolfram MathWorld. Combinatorics, Automata and Number Theory CANT. Combinatorics, Automata and Number Theory excerpt. ON THE DECIMAL EXPANSION OF ALGEBRAIC NUMBERS Siauliai. Mahler selecta. Chapter25.