

La galerie de portraits des mathématiciens. Les Partenaires de la Semaine des Maths. Gödel, Escher, Bach : Les Brins d'une Guirlande Éternelle. Arithm'Antique n°38 - Euclide et la philosophie du point. GDChapitre4: La projection de Monge. La projection de Monge. Séminaire Math-Philo 2019 (ENS Ulm) : Pierre Cartier, Hilbert et l'axiomatisation de la Physique. Matilde Martínez - Le théorème de Banach-Tarski, un paradoxe géométrique.
Souvenirs d'Alexander Grothendieck par Michel Demazure. Mandelbrot set images and videos. This page provides links to various (hopefully) pretty images and videos of the Mandelbrot set that I computed with a program I wrote.
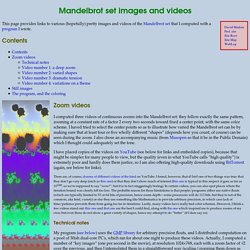
Contents Zoom videos I computed three videos of continuous zooms into the Mandelbrot set: they follow exactly the same pattern, zooming at a constant rate of a factor 2 every two seconds toward fixed a center point, with the same color scheme. I haved tried to select the center points so as to illustrate how varied the Mandelbrot set can be by making sure that at least four or five wholly different “shapes” (depends how you count, of course) can be seen during the zoom. I also chose an accompanying music (from Musopen so that it be in the Public Domain) which I thought could adequately set the tone.
There are, of course, dozens of different videos of the kind on YouTube. Géométriser l'espace : de Gauss à Perelman. Commençons au deuxième siècle... avant Jésus-Christ.Hipparque, et son successeur Ptolémée, trois siècles plus tard, sont semble-t-il, parmi les premiers à s’être posé la question de la “représentation” la plus précise possible du ciel étoilé ou de la surface de la terre sur un plan.
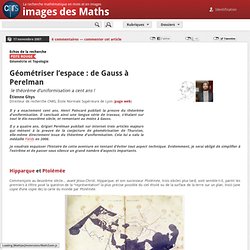
Voici (une copie d’une copie de) la carte du monde par Ptolémée. C’est le début de la cartographie scientifique. Parmi les méthodes introduites à cette époque, il faut mentionner la projection stéréographique. Médaille Fields : la France, 2e nation la plus récompensée, absente du palmarès 2018. Outre qu’elle se tenait pour la première fois dans l’hémisphère Sud, la cérémonie de remise des médailles Fields, prestigieux prix de mathématiques, a eu pour autre singularité de ne pas récompenser un Français, un fait inédit depuis près de trente ans.
Lire : Mathématiques : quatre nouvelles médailles Fields ouvrent de nouveaux chemins vers la connaissance Les Français ont longtemps été les enfants chéris des mathématiques en général et de cette récompense en particulier, la France étant la deuxième nation la plus primée de la médaille Fields. E. Ghys, les images comme symboles mathématiques. Mathematicians of the African Diaspora CONTENTS. Who are the greatest Black Mathematicians? : Les grands mathematiciens noirs. Peu connus du grand public, un certains nombre de mathématiciens noirs ont marqué leur époque.
Le plus grand est certainement David Blackwell, dont le travail peut être qualifié d’extraordinaire, mathématiquement parlant. Les autres ne sont pas loin derrière : il s’agit de J. Ernest Wilkins, Albert-T Barucha Reid, Georges O Okikiolu et James Ezeilo, Ronald J Mickens et Charles Bell. Sphéroïde de Clairaut. Le sphéroïde de Clairaut est un modèle de la forme de la Terre donné en 1743 par Alexis Clairaut.
Dans ce modèle, la Terre n'est plus une sphère parfaite, mais est aplatie aux pôles, conformément aux prévisions données par Isaac Newton en 1687. Par ce modèle, Clairaut contribue à imposer les idées de Newton en France, alors qu'elles y étaient encore contestées. Histoire et préhistoire de la Géométrie d'Arakelov. Géométrie d'Arakelov des surfaces arithmétiques. Diagramme de Voronoï. Un article de Wikipédia, l'encyclopédie libre.
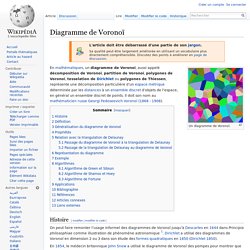
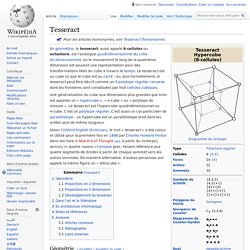
Histoire[modifier | modifier le code] On peut faire remonter l’usage informel des diagrammes de Voronoï jusqu'à Descartes en 1644 dans Principia philosophiae comme illustration de phénomène astronomique [1]. Dirichlet a utilisé des diagrammes de Voronoï en dimension 2 ou 3 dans son étude des formes quadratiques en 1850 (Dirichlet 1850). En 1854, le médecin britannique John Snow a utilisé le diagramme de Voronoï des pompes pour montrer que la majorité des personnes mortes dans l’épidémie de choléra de Soho se trouvaient dans la cellule de la pompe à eau de Broad Street, donc qu'ils vivaient plus près de cette pompe que de n’importe quelle autre pompe[2]. Il a ainsi démontré que le foyer de l'infection était cette pompe. Tesseract. Une généralisation du cube aux dimensions plus grandes que trois est appelée un « hypercube », « n-cube » ou « polytope de mesure ».
Math sup. Desmos: A Definitive Guide in Graphing and Computing. Think you’re fond of of graphing and computing stuffs?
The On-Line Encyclopedia of Integer Sequences® (OEIS®) Mathématiques : deux infinis différents sont en fait de même taille. Cette découverte va à l’encontre de ce que l'on pensait depuis des décennies : deux mathématiciens viennent de prouver que deux sortes différentes d’infini ont en réalité la même taille.
Cette avancée touche l’un des problèmes les plus célèbres et les plus insolubles des mathématiques : existe-t-il des types d'infinis de taille intermédiaire entre celle de l'ensemble des nombres entiers naturels et celle des nombres réels, plus grand ? Le problème a été identifié pour la première fois il y a un siècle. A cette époque, les mathématiciens savaient que « les nombres réels étaient plus nombreux que les nombres naturels », mais ils ne savaient pas de combien. « Est-ce juste la taille au dessus, ou existe-t-il une taille intermédiaire ? », explique Maryanthe Malliaris, de l’université de Chicago, coauteure de la nouvelle étude avec Saharon Shelah, de l’université hébraïque de Jérusalem et de l’université de Rutgers. Problèmes de Hilbert. Lors du deuxième congrès international des mathématiciens, tenu à Paris en août 1900, David Hilbert présenta une liste de problèmes qui tenaient jusqu'alors les mathématiciens en échec.
Ces problèmes devaient, selon Hilbert, marquer le cours des mathématiques du XXe siècle, et l'on peut dire aujourd'hui que cela a été grandement le cas. Publiée après la tenue du congrès, la liste définitive comprenait 23 problèmes, aujourd'hui appelés les problèmes de Hilbert. Cédric Villani, le boss des maths. Jean-Pierre Ramis - "Leonhard Euler, ou l'art de donner un sens à ce qui n'en avait pas". Singh:th_de_fermat-wiles. Grothendieck Circle. Writings/Écrits : Cédric Villani. J’ai regroupé dans cette page des écrits divers, composés pour des occasions variées : Textes de vulgarisation (contributions à des ouvrages scientifiques pour grand public), Cartes blanches pour le supplément Sciences du quotidien Le Monde; Tribunes et réflexions (réflexions liées à la recherche, témoignages pour grand public…), Préfaces et éditoriaux, Textes littéraires (exercices de style, textes destinés à des festivals ou rencontres…); enfin une liste d’ouvrages grand public.
Textes de vulgarisation. La Coss. Fonction continue nulle part dérivable. Un article de Wikipédia, l'encyclopédie libre. La continuité d'une fonction signifie que sa courbe représentative n'admet pas de « cassure ». Programme de Hamilton. Un article de Wikipédia, l'encyclopédie libre. Le programme de Hamilton est une idée de « plan d'attaque », due à Richard S.
Hamilton, de certains problèmes en topologie des variétés, notamment la célèbre conjecture de Poincaré. Courbure scalaire. Un article de Wikipédia, l'encyclopédie libre. En géométrie différentielle, la courbure scalaire (ou courbure de Ricci, ou scalaire de Ricci) est l'outil le plus simple pour décrire la courbure d'une variété riemannienne. Il assigne à chaque point d'une variété riemannienne un simple nombre réel caractérisant la courbure intrinsèque de la variété en ce point. Dans un espace à deux dimensions, la courbure scalaire caractérise complètement la courbure de la variété. En dimension ≥ 3, cependant, il n'y suffit pas et d'autres outils sont nécessaires. Plan projectif arguésien. Un article de Wikipédia, l'encyclopédie libre. LES LACS DE WADA - Images des mathématiques. Les frontières Commençons par un exemple très simple. Voici un disque dessiné dans le plan. Donald au Pays des Mathémagiques (1959) - Walt Disney - Le blog-notes mathématique du coyote.
Donald au Pays des Mathémagiques (1959) - Walt Disney. MathEnVille - Conférences grand public. The Center of Math Blog: Fun Friday: World Tesselation Day. "The geometry of space translates to a reoccurring theme in my creations: the tessellation. " - M.C EscherM.C Fisher was one of the artists responsible for leading the art of tessellation.
Today, June 17th, is M.C Escher's birthday. This served as the inspiration for Emily Grosvenor's push to create World Tessellation Day. Grosvenor is the author of a children's book about a girl named Tessa who sees patterns everywhere titled, Tessalation. What is a tessellation? MégaMaths Blog. Maths. Portail:Mathématiques. Une page de Wikipédia, l'encyclopédie libre. Les mathématiques, du grec máthēma (μάθημα) signifiant « connaissance, science », constituent un domaine de savoir, de recherche et d'enseignement, fondé sur le raisonnement logique.
Elles portent sur les nombres, les formes, les opérations et d'autres notions qui permettent entre autres de modéliser l'évolution dans le temps, les procédures, notamment en informatique, et même le hasard. Les mathématiques irriguent toutes les disciplines scientifiques et sont utilisées en économie ou dans les innovations technologiques, mais elles ont aussi des relations avec la philosophie, les arts plastiques, la musique et même les jeux et la littérature.
Branches des mathématiques. Bienvenue sur ChronoMath, une chronologie des mathématiques. Prix d'Alembert. Un article de Wikipédia, l'encyclopédie libre. Dictionnaire des mathématiques. Main Page - Encyclopedia of Mathematics. Archives Bourbaki. Math Encounters – The Museum of Mathematics. Semaine des Mathématiques. Voyage en Mathématique - Projet Voyage en Mathématique - Produits pédagogiques - Mathématiques - Fermat Science. Site de ressources scientifiques pour les enseignants de mathématiques. The Beauty of Mathematics: A Visual Demonstration of Math in Everyday Life. Wolfram MathWorld: The Web's Most Extensive Mathematics Resource. Web 2.0 scientific calculator.
GeoGebra. Un article de Wikipédia, l'encyclopédie libre. GeoGebra. TeX. TeX (/ˈtɛx/ or /ˈtɛk/, see below) is a typesetting system designed and mostly written by Donald Knuth[1] and released in 1978. Together with the Metafont language for font description and the Computer Modern family of typefaces, TeX was designed with two main goals in mind: to allow anybody to produce high-quality books using a reasonably minimal amount of effort, and to provide a system that would give exactly the same results on all computers, at any point in time.[2] TeX is a popular means by which to typeset complex mathematical formulae; it has been noted as one of the most sophisticated digital typographical systems in the world.[3] TeX is popular in academia, especially in mathematics, computer science, economics, engineering, physics, statistics, and quantitative psychology. It has largely displaced Unix troff, the other favored formatter, in many Unix installations, which use both for different purposes.
LaTeX. LaTeX (/ˈlɑːtɛx/ LAH-tekh or /ˈleɪtɛx/ LAY-tekh[1] styled as LaTeX, and a shortening of Lamport TeX) is a word processor and document markup language. It is distinguished from typical word processors such as Microsoft Office and LibreOffice in that the writer uses plain text as opposed to formatted text, relying on markup tagging conventions to define the general structure of a document (such as article, book, and letter), to stylise text throughout a document (such as bold and italic), and to add citations and cross-referencing.
Bienvenue sur Infinimath : Le Portail des mathématiques,Tangente - Editions POLE. Une revue produite par l'Institut des sciences mathématiques et le Centre de recherches mathématiques. Association Animath. Ordinaux. Les-Mathematiques.net - Cours de mathématiques supérieures. La vache. BricoMaths. Inclassables Mathématiques 2.0. Images des mathématiques. Le mathoscope. Société Mathématique de France. Paroles et blagues de matheux. Mathématiques. Mathématiques. Mathématiques. Mathématiques. Math. Géométrie. Géométrie. Géométrie euclidienne. Cévienne.
Théorème de Stewart. Loi des cosinus. Surfaces. Torsion d'une courbe. MATHCURVE.COM. Théorème isopérimétrique. Série de Fourier. Inégalité de Wirtinger. Fractale. Choux romanesco, Vache qui rit et intégrales curvilignes. Hairy ball theorem. Pavage de Penrose. Ernst.k a ajouté : Une définition mathématique de la frontière et de sa dimension. Ernst.k a ajouté : Stéphane Dugowson - Les frontières dialectiques. Ernst.k a ajouté : Frontière (topologie) Ernst.k a ajouté : Les mathématiques des frontières floues. Modélisation de mouvements de foules. Notation des flèches de Knuth. Gogolplex.