

Le saviez-vous? Voici une série de petites anecdotes à ajouter à la fin des devoirs ou à évoquer lors des cours pour sensibiliser les élèves à la culture historique des mathématiques....

Que si 11 se dit "onze"et non "dix-un" comme 17 se dit "dix-sept", c'est normal et cela s'explique bien. "Onze" provient de la contraction de undecim (littéralement un-dix) qui a évolué en "undece", à prononcer ounedécé et à dire rapidement on dira oundzé, très proche de onze, non? Cela marche aussi pour douze (duodecim), treize (tredecim) etc. Comment les maths ont vaincu Hitler. La théorie du Chaos - TPE. Étienne Ghys - Et si le théorème de Pythagore n'était pas vrai ? Mathematics Awareness Month - April 2014 - Geometrical Vanishes. Navigate the Calendar A geometrical vanish (or geometric vanish) is a puzzle comprising several pieces whose area seems to change according to how the pieces are arranged.
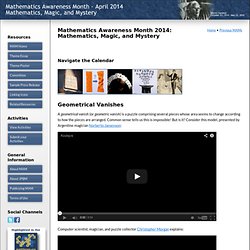
Common sense tells us this is impossible! But is it? Consider this model, presented by Argentine magician Norberto Jansenson: Computer scientist, magician, and puzzle collector Christopher Morgan explains: Download the template for the Martin Gardner dollar bill geometric vanish. Perhaps the most famous geometrical vanish was invented by the great Sam Loyd, an American puzzle creator whose Get Off the Earth puzzle reportedly sold over 10 million copies during his lifetime.
The puzzle based on rearranging the pieces of an 8×8 square to form a 5×13 rectangle is another classic, having first appeared in print in 1868, according to W.W. The rearrangement of the pieces of the chocolate bar to gain an “extra” square is another classic geometrical vanish. And once you understand that, can you fathom what’s happening here? Vauban pour les cochons comme Fibonacci pour les lapins.
Vauban fut un homme de guerre : ingénieur militaire, il dirigea 53 sièges, répara 300 places fortes et en construisit 33 nouvelles.
En 1703, il avait 70 ans, Louis XIV le nomma Maréchal de France. Il mourut de mort naturelle en 1706. Portrait de Vauban Vauban fut aussi un homme de cœur, soucieux du bien commun, et rédacteur infatigable de divers mémoires, dont ceux rassemblés en douze volumes sous le nom des « Oisivetés ou ramas de plusieurs sujets à ma façon ». Math in Real Life Series. La meilleure et la pire des erreurs de Poincaré.
La meilleure et la pire des erreurs de Poincaré 19/09/2012 17:00 | Durée 02:26:03 Intervenants :Christophe Besse , Directeur du Laboratoire Paul Painlevé, (CNRS / Université Lille 1) .
Françoise Paillous , Déléguée régionale CNRS Nord-Pas de Calais – Picardie . Marie-Jeanne Philippe , Recteur de l’Académie de Lille, Chancelier des Universités . Philippe Rollet , Président de l'Université Lille1 élu en 2007 et 2012, Représentant de la CPU, Directeur du laboratoire MEDEE UPRES-EA 1039 (Mécanismes Economiques et Dynamiques des Espaces Européens) de 1991 à 2005, docteur honoris causa Université de Timisoara, Chaire Jean Monnet . Rodolphe Turpault - "Modélisation mathématique, calcul scientifique et zombies" Zoom_Math2006_Bassedef. Dossier : les nombres premiers sous toutes les coutures. Merveilleux nombres premiers Très tôt, dès les premiers partages de jouets ou de friandises, on apprend que certains nombres entiers, tel 6 = 2 x 3, se « cassent » aisément en deux facteurs.
Le crible d’Ératosthène Pour connaître en une seule fois un grand nombre de nombres premiers consécutifs et pas trop grands (par exemple inférieurs à un milliard), on dispose d’une méthode vieille de plus de 2.000 ans. La décomposition en facteurs premiers Comme tout nombre entier supérieur à 1 est divisible par au moins un nombre premier, on comprend de façon intuitive que l’on peut ramener tout nombre entier à un produit où ne figurent que des nombres premiers. L’unicité de la décomposition en facteurs premiers Ce théorème « clé » est ce qui nous manquait pour prouver enfin le résultat d’unicité de la décomposition en facteurs premiers.
L’arithmétique modulaire et les nombres premiers Arithmétique modulaire : le petit théorème de Fermat L’histoire du plus grand nombre premier et nombres de Mersenne. Les statistiques mathématiques, leurs pièges, leurs succès. Entretien imaginaire*On dit : il y a trois degrés dans le mensonge : le mensonge simple, le fieffé mensonge et la statistique ; pourtant les statistiques sont souvent utiles, alors que faire ?

Le problème principal est-il le choix au départ de ce qu'on décide de compter, de mesurer, des questions qu'on pose ? Les pièges se situent certes en amont des recueils de chiffres, mais également dans ce recueil même, puis dans le traitement mathématique ou informatique des données, enfin en aval dans leur interprétation. Les erreurs et biais peuvent provenir d'un choix idéologique, d'une volonté de tromper, ou aussi d'une naïveté, d'un manque de culture statistique, car cette discipline est assez subtile. Les mathématiques, un outil indispensable pour l'innovation et les nouvelles technologies. Maria J.

Esteban, directrice de recherche au CNRS, explique pourquoi les mathématiques sont utiles au-delà de l’enseignement et au-delà du simple intérêt de l’avancement de la science et de la connaissance. On a beaucoup parlé récemment des mathématiques en France à cause du mauvais classement que celles-ci occupent dans la dernière Enquête Pisa 2012 sur l’enseignement dans les pays de l’OCDE. Michel Broué : "Le monde est régi par les maths"