

Integration and the fundamental theorem of calculus. Fermat, les prémices du calcul différentiel et optimisation - Fermat Science. Indeterminate: the hidden power of 0 divided by 0. Calcul infinitésimal (avec des "infiniment petits")- Numberphile. La première réception française du calcul leibnizien. La première réception française du calcul leibnizien 19/04/2018 12:00 | Durée 01:07:58 Loaded: 0% Progress: 0% Intervenants :Sandra Bella , Université de Nantes, Laboratoire Jean Leray/Laboratoire SPHERE .
Une histoire du calcul différentiel, de la dérivation et des tangentes. Naissance du concept de tangente Le célèbre mathématicien grec Archimède de Syracuse (-287 ; -212) le premier semble s'intéresser à la notion de tangente.
Il énonce des propriétés concernant notamment les tangentes à la spirale qui porte son nom. Des siècles plus tard, le mathématicien italien Torricelli (1608-1646) et le français Roberval (1602-1675) prolongent la méthode d'Archimède et apportent les premières pierres à un édifice majeur des mathématiques, le calcul infinitésimal. La tangente comme position limite Le mathématicien français Pierre de Fermat (vers 1610-1665), surnommé "prince des amateurs", décrit ensuite la tangente comme position limite d'une sécante à une courbe. L'école anglaise ... Les méthodes analytiques de Descartes et de Fermat ont beaucoup de succès en Angleterre et sont donc reprises par John Wallis (1616-1707) et James Gregory (1638-1675). Newton et Leibniz Vers plus de rigueur Le taux d'accroissement. What Is an Integral? What does area have to do with slope?
ISAAC NEWTON - sa vie - biographie. Marque le véritable début des mathématiques modernes : - calcul différentiel et mécanique céleste, notamment.
L’un des trois plus grands mathématiciens de tous les temps - avec Archimède et Gauss. Il invente la théorie du calcul intégral, en même temps que Leibniz (1646-1716) inventait le calcul différentiel. - Leibniz publie sa description de l’analyse en 1684. - Les mathématiciens d'Eudoxe à Fermat ont découvert des techniques de dérivation et d’intégration avant Newton et Leibniz. - Mais ils n’avaient pas vu la relation entre les deux. - Newton et Leibniz, travaillant séparément, établissent les règles générales pour toutes les fonctions. Fonction dérivée/Nombre dérivé. Début de la boite de navigation du chapitre fin de la boite de navigation du chapitre En raison de limitations techniques, la typographie souhaitable du titre, « Fonction dérivée : Nombre dérivé Fonction dérivée/Nombre dérivé », n'a pu être restituée correctement ci-dessus.
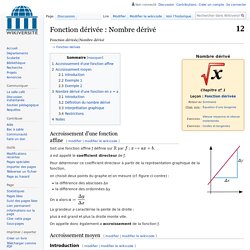
Accroissement d'une fonction affine[modifier | modifier le wikicode] Soit une fonction affine ƒ définie sur par a est appelé le coefficient directeur de ƒ. Calcul différentiel et intégral) Dernière mise à jour de ce chapitre: 2017-08-06 17:22:33 | {oUUID 1.684} Version: 3.2 Révision 7 | Avancement: ~95% vues depuis le 2012-01-01: 31'795 Le calcul différentiel est un des domaines les plus passionnants et vastes de la mathématique, et il existe une littérature considérable (colossale) sur le sujet.
Les résultats initiés par des scientifiques comme Fermat, Newton, Leibniz, Euler et compagnie depuis la fin du 17ème siècle retrouvent des implications dans absolument tous les domaines de la physique, de l'informatique, de l'électronique, de la chimie, de la finance, de la biologie et de la mathématique elle-même. Ce constat fait, nous avons choisi de ne présenter ici que les points absolument nécessaires à la compréhension des outils fondamentaux de l'ingénieur. Les puristes nous excuseront donc pour l'instant de ne pas présenter certains théorèmes qui peuvent leur sembler indispensables mais que nous rédigerons une fois le temps venu... Calcul infinitésimal (avec des "infiniment petits")- Numberphile. 1S Chapitres 03 et 04 CT. Dérivée. En mathématiques, la dérivée d'une fonction d'une variable réelle mesure l'ampleur du changement de la valeur de la fonction (valeur de sortie) par rapport à un petit changement de son argument (valeur d'entrée).
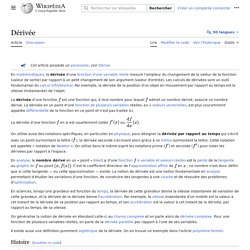
Les calculs de dérivées sont un outil fondamental du calcul infinitésimal. Par exemple, la dérivée de la position d'un objet en mouvement par rapport au temps est la vitesse (instantanée) de l'objet. La dérivée d'une fonction est une fonction qui, à tout nombre pour lequel admet un nombre dérivé, associe ce nombre dérivé. La dérivée d'une fonction en est usuellement notée ou On utilise aussi des notations spécifiques, en particulier en physique, pour désigner la dérivée par rapport au temps qui s'écrit avec un point surmontant la lettre ( ), la dérivée seconde s'écrivant alors grâce à un tréma surmontant la lettre. D'une fonction au point . On généralise la notion de dérivée en étendant celle-ci au champ complexe et on parle alors de dérivée complexe. Si on se donne une abscisse Soit.