Exponential growth and epidemics

La beauté de la multiplication Question : faut-il être fou pour parler d'arithmétique modulaire à un collégien ?Réponse : non ! On l'utilise même tous les jours en regardant l'heure... L'idée de base de l'arithmétique modulaire est de travailler non sur les nombres eux-mêmes, mais sur les restes de leur division par quelque chose.Par exemple, s’il est 16h52 et que j’attends 15 minutes, il sera 17h07, autrement dit 52+15=7 dans l’arithmétique (des minutes) de l’horloge. La première réception française du calcul leibnizien La première réception française du calcul leibnizien 19/04/2018 12:00 | Durée 01:07:58 Loaded: 0% 0le Monde _ Les Décodeurs_ Qu’est-ce que le « R0 », le taux de reproduction du virus ? Alors que l’on s’interroge sur le risque de rebond de l’épidémie de Covid-19, le R0 est l’une des valeurs les plus surveillées en France et à l’étranger. Ce chiffre, qui est l’un des principaux indicateurs utilisés par les épidémiologistes, doit être interprété avec précaution. Le R0, un indicateur reposant sur trois facteurs Prononcé « R zéro », le R0, ou nombre de reproduction de base, indique le nombre moyen de nouveaux cas d’une maladie qu’une seule personne infectée et contagieuse va générer en moyenne dans une population sans aucune immunité (on appelle les gens sans immunité des personnes susceptibles). Le R0 du Covid-19 était estimé début 2020, d’après les données de l’épidémie en Chine, à 3,28 en moyenne, un chiffre calculé d’après douze estimations différentes dans une revue de la littérature publiée dans le Journal of Travel Medicine. Cela signifie qu’en Chine, une personne infectée par le coronavirus SARS-CoV-2 aurait infecté en moyenne 3,28 nouvelles personnes.

Epicycles de Ptolémée Epicycles de Ptolémée Pour les grecs depuis Aristote (−385, −322) la Terre était le centre du Monde. Seul Aristarque de Samos (−310, −230) avait envisagé un système héliocentrique. Fonction dérivée/Nombre dérivé Début de la boite de navigation du chapitre fin de la boite de navigation du chapitre En raison de limitations techniques, la typographie souhaitable du titre, « Fonction dérivée : Nombre dérivé Fonction dérivée/Nombre dérivé », n'a pu être restituée correctement ci-dessus. Accroissement d'une fonction affine[modifier | modifier le wikicode]

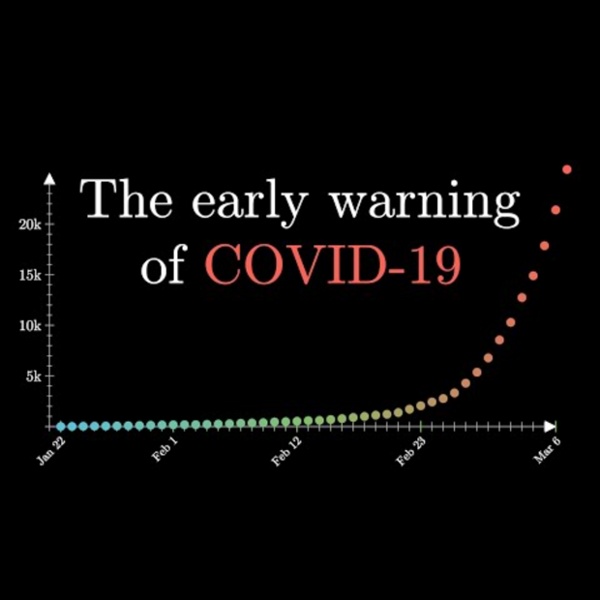
Covid-19 : décoder les chiffres du coronavirus Data science vs fake Diffusé le 1 avril 2020 Depuis le début de l’épidémie de Coronavirus, les chiffres pleuvent. Le nombre de malades, de décès, les modes de transmission ou la période d’incubation : que nous disent réellement ces données ? Comment décoder et bien comprendre ces statistiques ? Un numéro spécial de la série « Data science vs Fake, saison 2 ». Dérivée En mathématiques, la dérivée d'une fonction d'une variable réelle mesure l'ampleur du changement de la valeur de la fonction (valeur de sortie) par rapport à un petit changement de son argument (valeur d'entrée). Les calculs de dérivées sont un outil fondamental du calcul infinitésimal. Par exemple, la dérivée de la position d'un objet en mouvement par rapport au temps est la vitesse (instantanée) de l'objet.

Épidémie, nuage radioactif et distanciation sociale Le but de ce billet (un peu inhabituel) est d’illustrer de façon simple l’incroyable efficacité potentielle des mesures de distanciation sociale (limiter les rencontres, hygiène, télétravail, fermeture des écoles…) lorsque l’on est face à une épidémie qui vire à la pandémie. Une épidémie est une réaction en chaîne, et cela change tout sur l’impact potentiel de mesures de ce type, par rapport à d’autres sources de danger. Pour bien le comprendre, imaginons une autre situation : supposons que l’on ne soit pas face à une épidémie, mais à un danger d’un autre type, disons un nuage radioactif (ou chimique). Du fait de la présence du nuage, imaginons qu’il devienne risqué de sortir, que cela puisse nous rendre malade, voire à terme nous tuer. (Et supposons qu’enfermés chez soi on ne craigne rien).

calcul différentiel et intégral) Dernière mise à jour de ce chapitre: 2017-08-06 17:22:33 | {oUUID 1.684} Version: 3.2 Révision 7 | Avancement: ~95% vues depuis le 2012-01-01: 31'795 Le calcul différentiel est un des domaines les plus passionnants et vastes de la mathématique, et il existe une littérature considérable (colossale) sur le sujet. Les résultats initiés par des scientifiques comme Fermat, Newton, Leibniz, Euler et compagnie depuis la fin du 17ème siècle retrouvent des implications dans absolument tous les domaines de la physique, de l'informatique, de l'électronique, de la chimie, de la finance, de la biologie et de la mathématique elle-même. Ce constat fait, nous avons choisi de ne présenter ici que les points absolument nécessaires à la compréhension des outils fondamentaux de l'ingénieur. Les puristes nous excuseront donc pour l'instant de ne pas présenter certains théorèmes qui peuvent leur sembler indispensables mais que nous rédigerons une fois le temps venu...