

Calculus Rhapsody. Entretien avec Wendelin Werner, mathématicien et médaille Fields 2006. Peut-on modéliser une foule mathématiquement? Micmaths - L'élégance en mathématiques. Jean Mawhin : Surprises et beautés en passant du réel au complexe. La Théorie des Jeux — Science étonnante #39. Henri Cartan une vie de mathématicien. Jean-Pierre Serre, Pierre Cartier, Jacques Dixmier & Alain Connes - Bourbaki, les années 1945-75. Alexandre Grothendieck: l'équivalent d'Einstein en maths. Il explique pourquoi il décide de tout quitter. Alexander Grothendieck: Documentaire. Confidences de Grothendieck : "Einstein" méconnu des maths. La face cachée des tables de multiplication - Micmaths. La même en anglais ! Times Tables, Mandelbrot and the Heart of Mathematics.
Multiplication modulaire. Beauté des tables de multiplication. La beauté de la multiplication. Question : faut-il être fou pour parler d'arithmétique modulaire à un collégien ?
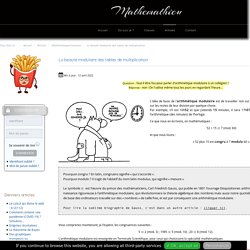
Réponse : non ! On l'utilise même tous les jours en regardant l'heure... L'idée de base de l'arithmétique modulaire est de travailler non sur les nombres eux-mêmes, mais sur les restes de leur division par quelque chose.Par exemple, s’il est 16h52 et que j’attends 15 minutes, il sera 17h07, autrement dit 52+15=7 dans l’arithmétique (des minutes) de l’horloge. Ce que nous en écrivons, en mathématiques : 52 + 15 ≡ 7 (mod. 60) et que nous lisons : « 52 plus 15 est congru à 7 modulo 60 ». Pourquoi congru ? Pour lire la sublime biographie de Gauss, c'est dans un autre article : cliquer ici. Vous comprenez maintenant, je l’espère, les congruences suivantes : 5 ≡ 2 (mod. 3) ; 1985 ≡ 5 (mod. 10) ; 20 ≡ 8 (mod. 12). L’arithmétique modulaire est enseignée en Terminale Scientifique, pour ceux qui choisissent la spécialité mathématiques.Autant dire à des années de ce que pourrait comprendre un élève de collège…
Péndulo de Pintura. La beauté des maths et de la physique avec un PENDULE! Sand pendulums - Lissajous patterns: courbes de Lissajous, PENDULES de sable. Le pendule de Foucault : explication et démonstration. Ce professeur risque sa mâchoire pour démontrer un principe physique ! Epicycloïdes. Ptomolée beaucoup plus fort que Pythagore! Epicycles de Ptolémée.
Epicycles de Ptolémée Pour les grecs depuis Aristote (−385, −322) la Terre était le centre du Monde.
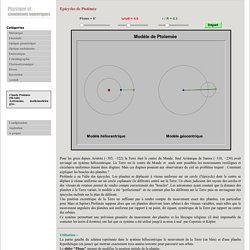
Seul Aristarque de Samos (−310, −230) avait envisagé un système héliocentrique. La Terre est le centre du Monde et seuls sont possibles les mouvements rectilignes et circulaires uniformes étaient deux dogmes. Mais ces dogmes posaient aux observateurs du ciel un problème majeur : Comment expliquer les boucles des planètes ? Ptolémée a eu l'idée des épicycles. Utilisation : La partie gauche du schéma représente dans le système héliocentrique le mouvement de la Terre (en bleu) et d'une planète hypothétique (en jaune) qui mettrait exactement trois années terrestre pour parcourir son orbite. Le slider rouge permet de modifier le rapport des vitesses de rotation entre l'épicycle et le déférent. Funny Fractions and Ford Circles - Numberphile. Indeterminate: the hidden power of 0 divided by 0. Exponential growth and epidemics. Freaky Dot Patterns - Etranges motifs avec des points. Fascinant! LMS Popular Lecture Series 2008, Toy models, Dr Tadashi Tokieda.
Les fractales, un outil pour comprendre le monde. FRACTALE:The Hardest Mandelbrot Zoom in 2017 - New record, 750 000 000 iterations! Alan Turing - Enigma, ordinateur et pomme empoisonnée - LPPV.05 - e-penser. La drôle de guerre d'Alan Turing... Nos algorithmes pourraient-ils être BEAUCOUP plus rapides ? (P=NP ?) L'Hypothèse de Riemann — Science étonnante #62. La conjecture de Syracuse - Deux (deux ?) minutes pour... La fourmi de Langton — Science étonnante #21.
The mathematical secrets of Pascal’s triangle - Wajdi Mohamed Ratemi. What Makes People Engage With Math. Le Jeu de la Vie — Science étonnante #49. Epic conway's game of life. Deux (deux ?) minutes pour John Conway. Le repliement des protéines : Résolu par l'intelligence artificielle AlphaFold ? Eratosthène - Mesurer la Terre avec un bâton et un chameau.
Expériences de supraconductivité (mécanique quantique) La Plus Belle Expérience de la Physique (mécanique quantique) Les inégalités de BELL & les expériences d'Alain ASPECT. La Dualité Onde-Corpuscule. The Fantastic Mr. Feynman. Qu'y avait-il avant le Big Bang ? Par Aurélien Barrau. Qu'est que le temps : vision cosmologique. A. Barrau, colloque de Nice.
Le mystère des gâteaux quantiques. Qu'y avait-il avant le Big Bang ? Sommes-nous seuls dans l'Univers ? — Le paradoxe de Fermi [Astrobiologie #3] La plus grosse erreur de l'histoire de la physique — Science étonnante #11. E=mc² et le boson de Higgs — Science étonnante #46. LHC: le plus grand accélérateur de particules. Le Boson de Higgs. Une nouvelle façon d'illustrer la Relativité Générale. La Théorie de Relativité Restreinte d'Einstein — Science étonnante #45. Le paradoxe des jumeaux : rajeunir à la vitesse de la lumière ? La Relativité Générale — Science étonnante #56.