

Le nombre d'or - Micmaths. Images des mathématiques. Avez-vous déjà entendu parler du nombre d’or ?

Très probablement. Comment le définissez-vous ? En posant cette question autour de moi, j’ai reçu diverses réponses : « il gouverne les spirales des ananas et des pommes de pin », « c’est la proportion de la façade du Parthénon », « c’est un rapport caché dans la pyramide de Kheops », « c’est grâce à lui que le sourire de la Joconde est si mystérieux », « c’est un plus racine carrée de cinq divisé par deux ». Ou, en symboles, . Là, vous l’auriez parié, c’est un mathématicien qui répliquait. Cette réponse est correcte, mais elle ne permet pas de pressentir pour quelle raison ce nombre a pu être comparé à l’or.
L’appellation « nombre d’or » est en fait récente, elle ne date que du début du XIX-ème siècle. Extrême et moyenne raison Avant la Renaissance, on parlait plutôt, plus lourdement, de « section en extrême et moyenne raison ». DM nb d'or 2nd degré. Suite de Fibonacci dans la nature. Loi Les bourgeons tenteraient de disposer du maximum de lumière et de place.

Le premier se place. Le second se positionne à un peu plus de 120°, en fait: Et les suivants tentent de conserver cet espacement de 137,5°. Voir Méristème apical Tableau Illustration Voilà, le sixième qui se trouve un peu à l'ombre du premier pétale. Moins de 50° pour se loger (32,5°). Est-ce la bonne raison ? C'est en tout cas ce que l'on peut lire dans quelques ouvrages sur le sujet. De nombreuses simulations sont faites pour retrouver à partir de telles hypothèses les dispositions en spirale des tournesols, des feuilles sur les tiges, des dessins du chou-fleur … Vocabulaire Foliation ou Phyllotaxie: disposition des feuilles sur la tige. Phyllotaxis: anglais pour foliation, leaf arrangement. Le nombre d'or dans la nature - Les fleurs et leurs pétales.
La suite de Fibonacci dans les fleurs Dans la nature après avoir observé plusieurs plantes,on constate que peu de fleurs présentent un nombre de pétales égal à 4 ,6 ou 7 et que la plupart présentent un nombre de pétales égal à 1 ,2 ,3 ou 5.
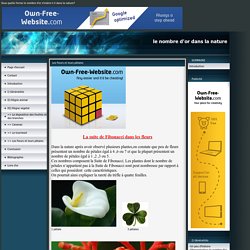
La suite de Fibonacci. Les lilas ont 3 pétales, les boutons d'or en ont 5, le pied d'alouette en a 8, l'aster en a 13 et les chicorées en ont 21.
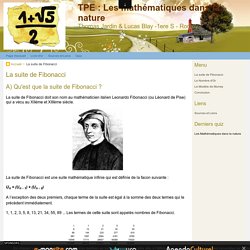
Les différentes espèces de marguerites ont 21, 34, 55 ou 89 pétales. Au cœur des tournesols, on remarque deux séries de courbes de graines, une enroulée dans un sens et une dans l'autre; le nombre de spirales n'étant pas le même dans chaque sens mais souvent une paire de termes de la suite de Fibonacci : 21-34, 34-55, 55-89. Comment monter un escalier - Micmaths. Le nombre d'or. Fruits d'Eucalyptus provenant de Galice en Espagne.

On trouve des pentagones réguliers, mais aussi des carrés er des triangles équilatéraux. Lien avec l'ensoleillement Cela vient de ce que l'ensoleillement doit être maximum pour toutes les feuilles et on démontre que l'angle de deux feuilles consécutives doit être voisin d'un certain k ème de tour ; les fractions de Fibonacci sont les fractions les plus voisines de k. Les graines dans une fleur de tournesol Ammonite L'enroulement régulier d'une ammonite se fait suivant une spirale logarithmique. La découverte des quasicristaux, de molécules en forme de dodécaèdre (constitué de 12 pentagones), de certains virus ayant cette forme montre que la symétrie d'ordre cinq est assez fréquente dans la nature. The fabulous Fibonacci flower formula. Pentagons and the Golden Ratio - Numberphile. Nature by Numbers.
Le nombre d'or. L'Homme de Vitruve de Léonard de Vinci Un nombre étonnant, mystérieux et magique pour avoir fait parler de lui depuis la plus haute antiquité dans de nombreux domaines tels que la géométrie, l’architecture, la peinture, la nature, … Il serait une expression d’harmonie et d’esthétique dans les arts bien que certains lui reproche son caractère ésotérique qui cherche absolument à lui trouver une obscure beauté et qui semble y parvenir ! On le note φ (phi) en hommage au sculpteur grec Phidias (Ve siècle avant J.C.) qui participa à la décoration du Parthénon sur l’Acropole à Athènes. Quant à son nom, il a évolué avec le temps. Le mathématicien et moine franciscain Luca Pacioli (1445 ; 1517) parle de « Divine proportion », plus tard le physicien Johannes Kepler (1571 ; 1630) le désigne comme le « joyau de la géométrie ». Alors que pour Léonard de Vinci, ce sera la « section dorée ».
On retrouve des traces du nombre d’or bien avant les grecs. Est sa valeur exacte. Le rectangle d'or. Le nombre d'or. (Vitruve, architecte romain 1er siècle avant notre ère). Ainsi si a et b sont les deux grandeurs alors nous aurons : a/b = (a + b) / a. A/b = 1 + b/a pour simplifier, prenons comme variable x = a/b. alors nous obtenons : x = 1 + 1/x x - 1 - 1/x = 0 comme x non nul, nous obtenons l'équation suivante que nous noterons (E) : x2 - x - 1 = 0 qui admet comme racine positive : x = que nous notons Φ et vaut à peu près 1,618...
Music From The Fibonacci Sequence. Le Nombre d'Or - Chronique Spéciale. Arithm'Antique n°6 - Le nombre d'or. Images des mathématiques. Le 2 septembre 2019 - Ecrit par Fernando Corbalán Cet article a été écrit en partenariat avec L’Institut Henri Poincaré Lire l'article en En 2013, l’Institut Henri Poincaré et Images des Mathématiques ont uni leurs efforts pour superviser la réédition de la collection Le monde est mathématique, publiée par RBA en partenariat avec Le Monde.
En 40 ouvrages, cette collection de qualité, issue d’un projet collectif de mathématiciens espagnols, vise à présenter, à travers une grande variété de points de vue, de multiples facettes des sciences mathématiques, sous un aspect historique, humain, social, technique, culturel ... Reprise et améliorée au niveau de la forme, cette édition a été entièrement lue et corrigée par l’équipe d’Images des Mathématiques ; des préfaces et listes bibliographiques ont été ajoutées. En 2019, cette collection est de nouveau éditée, présentée par Étienne Ghys et distribuée par L’Obs.
Extrait du Chapitre 1 Un monde doré Le secret des roses Sommaire du livre. Le nombre d'or. L' histoire ...

Dossier - La suite de Fibonacci et le nombre d'or - Podcast Science. Disclaimer : Ouh-la, cet article du tout début de notre site est un peu étrange !
On s’était apparement laissé un peu avoir par la nombre-d’or-mania et, avec quelques années de recul, on est pas extrêmement fier de son contenu. On vous propose donc plutôt d’aller voir ce billet de l’excellent blog Choux romanesco, Vache qui rit et intégrales curvilignes intitulé Le plus doré de tous les nombres qui en parle bien mieux que nous le faisons ici.
L’équipe de Podcast Science Dossier de Mathieu dans l’épisode #28. La suite de Fibonacci doit son nom au mathématicien italien Leonardo Fibonacci qui a vécut au XIIème et XIIIème siècle. Mais il est aussi connu pour avoir mis en évidence une suite mathématique qui porte désormais son nom. Il suffit de prendre deux nombres de départ. La suite de Fibonacci possède de nombreuses propriétés très utilisées en mathématiques. Collection de nombres, nombre d'or, divine proportion,section dorée. Nombre d'or - ce qu'il faut savoir en bref. Étapes de construction 1) Je construis un carré ABCD de 10 carreaux de côté. 2) Je positionne le point milieu M, en bas. 3) Je dessine un cercle de centre M et de rayon MB; il coupe la droite DC en F. 4) Le rectangle ABEF est un rectangle d'or.

Mesures et conclusions. The Golden Ratio (why it is so irrational) - Numberphile. Le nombre d'or. L'Homme de Vitruve de Léonard de Vinci Un nombre étonnant, mystérieux et magique pour avoir fait parler de lui depuis la plus haute antiquité dans de nombreux domaines tels que la géométrie, l’architecture, la peinture, la nature, … Il serait une expression d’harmonie et d’esthétique dans les arts bien que certains lui reproche son caractère ésotérique qui cherche absolument à lui trouver une obscure beauté et qui semble y parvenir !
On le note φ (phi) en hommage au sculpteur grec Phidias (Ve siècle avant J.C.) qui participa à la décoration du Parthénon sur l’Acropole à Athènes. Quant à son nom, il a évolué avec le temps. Nombre d’or. Définition, traduction, prononciation, anagramme et synonyme sur le dictionnaire libre Wiktionnaire. Français[modifier] Étymologie[modifier] (Mathématiques) Calque de l’allemand goldener Schnitt, lui-même utilisé par Martin Ohm en 1835. (Astronomie) Calque du latin numerus aureus. Le Nombre d'Or - Histoire. Fibonacci Mystery - Numberphile. Random Fibonacci Numbers - Numberphile. TPE : Le nombre d'or dans la nature, ou et pourquoi ? A.Croissance des plantes et Fibonacci - B. Phyllotaxie - C. Quelques exemples de plantes C).Quelques exemples de plantes ou l'on retrouver phi On retrouve un peu partout j dans la nature, grâce au nombres de la suite.
Nombre d'or et art : mythe ou réalité ? Juin 2006 Depuis l'Antiquité, artistes et philosophes croient à l'existence d'une proportion privilégiée permettant d'obtenir harmonie et beauté. C'est à Euclide que l'on doit les premières traces écrites du fameux nombre d'or. Il vaut (1 + v¬5)/2, soit environ 1,6. A l'époque, il s'appelle Phi. Phi revient à la mode à la Renaissance sous le nom de divine proportion, puis section dorée, et finalement nombre d'or.