

Questionnaire-pro : solution pour enquetes et sondages en ligne. Un peu de technique - Sondages CE : Sondages Comités d'entreprise. Pour déterminer la taille d'un l'échantillon adéquat, nous nous basons pour la plupart des études sur une loi de Bernouilli, laquelle fait intervenir 3 paramètres : sa représentativité, son homogénéité et sa précision.
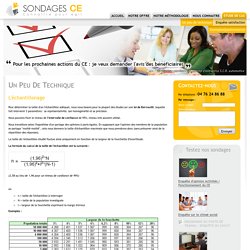
Nous pouvons fixer le niveau de l'intervalle de confiance de 95%, niveau très souvent utilisé. Nous travaillons selon l'hypothèse d'un partage des opinions à parts égales. En supposant que l'opinion des membres de la population se partage "moitié-moitié", cela nous donnera la taille d'échantillon maximale que nous prendrons donc (sans présumer ainsi de la répartition des réponses). Taille d'un échantillon aléatoire et Marge d'erreur. Introduction Lorsque l’on effectue une enquête on s’intéresse à une population mère (population totale) dont on va généralement interroger une petite partie, c’est l’échantillon dont il faut déterminer la taille soigneusement car elle a une grande importance sur la précision des estimations réalisées sur les caractéristiques de la population-mère.
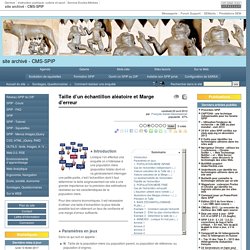
Pour des raisons économiques, il est nécessaire d’utiliser une taille d’échantillon la plus réduite possible tout en obtenant un taux de confiance et une marge d’erreur suffisants. Paramètres en jeux Dans ce qui suit on appelle : On définit également : Le Taux de sondage R = n/N La Fourchette d’incertitude I = 2e. La théorie statistique fourni les équations qui expriment les relations entre ces paramètres. Les Taux de confiance « s » les plus utilisés et les Coefficients de marge « t » associés sont donnés dans le tableau suivant : Cas de l’échantillon indépendant (non exhaustif) et sa réciproque Valeurs calculées de la Taille de l’échantillon « n » soit. Taille de l'échantillon de sondage - Évaluez le nombre de personnes à interroger. Comment calculer un intervalle de confiance: 6 étapes. En statistiques, un intervalle de confiance permet d'établir la marge d'erreur entre les données d'un sondage (échantillon) et les données de la population totale.
En effet, si votre population est vaste (plusieurs milliers de données), il est plus rapide de travailler sur un échantillon et d'étendre les résultats à l'ensemble. Bien sûr, il y a risque d'erreur, d'où cet indicateur qu'est l'intervalle de confiance avec sa marge d'erreur. Si vous suivez pas à pas les instructions ci-dessous, vous allez pouvoir évaluer la marge d'erreur de telle ou telle affirmation portant sur un échantillon.
Publicité Étapes <img alt="Image intitulée Calculate Confidence Interval Step 1" src=" width="670" height="503" class="whcdn">1Inscrivez le fait que vous voulez évaluer. <img alt="Image intitulée Calculate Confidence Interval Step 6" src=" width="670" height="503" class="whcdn">6Il ne reste plus qu'à établir l'intervalle de confiance. Conseils Eléments nécessaires. Intervalle de confiance. Un intervalle de confiance doit être associé à un niveau, en général sous la forme d’un pourcentage, qui minore la probabilité de contenir la valeur à estimer.
Par exemple, un sondage auprès de 1000 personnes sur une question fermée (où l’on ne peut répondre que par « oui » ou par « non »), est valable à plus ou moins 3 points de pourcentage, au niveau de 95 % (c’est-à-dire que cette marge n’est pas valable moins d’une fois sur 20). Pour obtenir un intervalle plus réduit, donc plus précis, sans changer le nombres de sondés, il faut accepter un niveau plus faible, donc un plus grand risque de se tromper. Au contraire, pour réduire le risque d’erreur, on peut élargir l’intervalle. Mathématiquement, un intervalle de confiance est modélisé par un couple de variables aléatoires qui encadrent un paramètre réel, et ne doit pas être confondu avec l'intervalle de fluctuation, qui est déterminé par le paramètre et encadre une variable aléatoire. Si on cherche à évaluer quelle proportion . Et. . , où. Tirage au sort sans remise d'un nom extrait d'une liste.
SURISTAT.