

Control - What are good strategies for tuning PID loops? - Robotics Stack Exchange. I'll try to expand a little from my experience for those who may be interested.
I think the problem is we have a lot of control theory that is somewhat inaccessible (and sometimes not useful) and then we have rules of thumb that make assumptions about systems that are often inaccurate. Stability Let's talk first about why control loops become unstable. For this discussion I'll assume a linear system. Informally this means that if your control signal is a sine wave at a given frequency then your observed output is at the same frequency and if you change the amplitude of your control system your output responds at the same ratio. Implementation of Fuzzy Self-Tuning PID and Feed-Forward Design for High-Performance Motion Control System. TY - JOUR T2 - International Journal of Fuzzy Logic and Intelligent Systems AU - Thinh, Ngo Ha Quang AU - Kim, Won-Ho SN - 1598-2645 TI - Implementation of Fuzzy Self-Tuning PID and Feed-Forward Design for High-Performance Motion Control System VL - 14 PB - Korean Institute of Intelligent Systems DO - 10.5391/IJFIS.2014.14.2.136 PY - 2014 UR - ER - Thinh, N.

H. Q. , & Kim, W. H. ( 2014). Controls & Instrumentation content from Hydraulics & Pneumatics. By Peter Nachtwey, Delta Computer Systems, Inc.
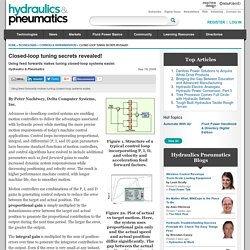
Advances in closedloop control systems are enabling motion controllers to deliver the advantages associated with hydraulic power while meeting the more precise motion requirements of today's machine control applications. Control loops incorporating proportional, integral, and differential (P, I, and D) gain parameters have become standard functions of motion controllers, and control algorithms have evolved to include additional parameters such as feed forward gains to enable increased dynamic system responsiveness while decreasing positioning and velocity error. The result is higher performance machine control, with longer machine life, due to smoother motion. Motion controllers use combinations of the P, I, and D gains in generating control outputs to reduce the error between the target and actual position.
ServoFundamentals. Control Theory Terminology. A trapezoidal velocity profile is adequate for most applications.
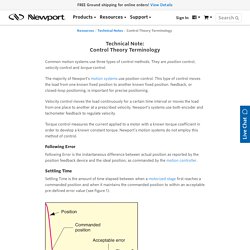
Its only disadvantage is that it may cause some system disturbances at the “corners” that translate in small vibrations, which extend the settling time. For demanding applications sensitive to this phenomenon, the velocity profile can be modified to have an S shape during the acceleration and deceleration periods. Arduino - Control both Velocity and Position (Linear actuator) - Robotics Stack Exchange. Control Engineering. Patrick Dixon, PE Despite being ubiquitous in industrial control system (ICS) usage, the proportional-integral-derivative (PID) algorithm is a mystery to many.

Ask an engineer to describe the behavior of the D (derivate) term, for instance, and some may respond with a blank stare. Textbooks, seminars, and articles often explain the PID control algorithm in a form resembling the following equation: The terms are: E = Error, difference between setpoint and measurement OP = Output to the final control element, typically in percent of scale P = Proportional term I = Integral term D = Derivative term Kp = Proportional gain Ki = Integral gain Kd = Derivative gain. Feed forwards augment PID control
Peter Nachtwey Feed forward augmentation is a prediction technique that estimates the output from a proportional-integral-derivative (PID) control algorithm without waiting for the PID algorithm to respond.

If the feed forward prediction can estimate the control output closely, the PID algorithm, whose job it is to minimize the error between the current state of the system and the desired state, will need to do less to correct the error. This reduces the error faster or keeps the error smaller than relying on the PID algorithm alone. Feed forward control outputs usually are calculated using the setpoint value and its derivatives (based on target velocity and acceleration values) and multiplying each one by a gain.
Understanding Backlash and Stiction. By Kristin Lewotsky, MCA Contributing Editor Motion Control & Motor Association Posted 01/13/2014 Learn how to compensate for lost motion that can prevent your system from performing as designed.

By definition, motion control involves taking a load from point A to point B in some specified time and with some specified absolute accuracy. In theory, a drive train combining motor, drive, gearbox, encoder, and actuator will act to move the load in a deterministic fashion—specify the right parameters and you get the right performance. The problem is that a motion system does not operate in theory, it operates in the real world, where it is subject to effects like backlash and stiction.
Friction. Index. Peter Nachtwey Feed forward augmentation is a prediction technique that estimates the output from a proportional-integral-derivative (PID) control algorithm without waiting for the PID algorithm to respond.

If the feed forward prediction can estimate the control output closely, the PID algorithm, whose job it is to minimize the error between the current state of the system and the desired state, will need to do less to correct the error. This reduces the error faster or keeps the error smaller than relying on the PID algorithm alone. Feed forward control outputs usually are calculated using the setpoint value and its derivatives (based on target velocity and acceleration values) and multiplying each one by a gain.
There are two types of motion control engineers: Those who are comfortable tuning a servo loop, and those who aren't. There are two types of motion control engineers: Those who are comfortable tuning a servo loop, and those who aren't.
The latter basically, have two options. The first is to use a non-servo device such as a stepmotor; the alternative, a better idea, is to get comfortable. Whether you're a novice or an experienced hand with servo tuning, this article can help you become more proficient when applying PID (proportional, integral, derivative) based servo loops. For starters, it explains two standard manual tuning methods that work well for many systems.
It also covers an ever more common remedy to manual tuning, autotuning, which despite its name, isn't necessarily as automatic as one would hope. Improving the Beginner’s PID – Introduction « Project Blog. In conjunction with the release of the new Arduino PID Library I’ve decided to release this series of posts.
The last library, while solid, didn’t really come with any code explanation. This time around the plan is to explain in great detail why the code is the way it is. I’m hoping this will be of use to two groups of people: People directly interested in what’s going on inside the Arduino PID library will get a detailed explanation. Anyone writing their own PID algorithm can take a look at how I did things and borrow whatever they like. It’s going to be a tough slog, but I think I found a not-too-painful way to explain my code.
Tuning Examples. Click on the graph to see it enlarged in a new window. Open loop test From this we determine process gain, delay time etc and can estimate... Zeigler-Nichols settings which almost invariably have too litttle gain and/or integral action Too little integral action, i.e. too large an reset time, is characterised by a sluggish return to the setpoint, here zero on the graph. Too much gain or integral. Panasonic Tech Insights: Electronic Components, Factory Automation and Lighting Solutions Articles. Tuning a control loop – PID – is the adjustment of its control parameters (gain/proportional band, integral gain/reset, derivative gain/rate) to the optimum values for the desired control response. Stability (bounded oscillation) is a basic requirement, but beyond that, different systems have different behavior, different applications have different requirements, and requirements may conflict with one another.
PID tuning is a difficult problem, even though there are only three parameters and in principle is simple to describe, because it must satisfy complex criteria within the limitations of PID control. There are accordingly various methods for loop tuning, and more sophisticated techniques are the subject of patents; this section describes some traditional manual method for loop tuning.
Manual Tuning If the system must remain online, first set Ti and Td values to zero*. Am06-pid_16Sep06. PID Controller For Lego Mindstorms Robots. A PID Controller is a common technique used to control a wide variety of machinery including vehicles, robots and even rockets. The complete mathematical description of a PID Controller is fairly complex but a much simpler understanding is really all that is needed to use a PID effectively.
This document is a description of how to create a PID Controller for use with Lego Mindstorms Robots using the NXT-G programming language. It will be easier if we have an actual task in mind so I will describe how to create a PID to do line following. Once created, the same PID can be used, with only minor modifications, with any other Mindstorms application such as getting a robot that can drive as straight as possible, or even for a robot that can balance with nothing but 2 wheels touching the ground like a Segway. .%5CInstellingenRegelaars_ExtraStof. Applications: Cellular Remote Monitoring. Anatomy Of A Feedback Control System Here is the classic block diagram of a process under PID Control.
What’s going on this diagram? Discrete PID Controller. Make a PI controller on an 8-bit micro. PID controller. Some applications may require using only one or two actions to provide the appropriate system control. This is achieved by setting the other parameters to zero. A PID controller will be called a PI, PD, P or I controller in the absence of the respective control actions. PI controllers are fairly common, since derivative action is sensitive to measurement noise, whereas the absence of an integral term may prevent the system from reaching its target value due to the control action. History and applications[edit] PID theory developed by observing the action of helmsmen. Discrete PID Controllers. Before discussing the design of digital control algorithms, let us consider discrete equivalents of analog controllers.
PIDTuningClassical - ControlsWiki. From ControlsWiki. Applications: Cellular Remote Monitoring. BackEMF. Introduction to Closed-Loop Control. PID-without-a-PhD.pdf. PID controller.