

Políedres amb brics. Els brics de suc, llet, brou, etc, són un bon material per construir políedres.
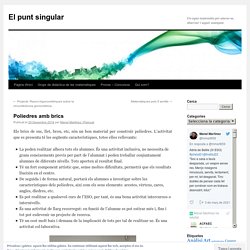
L’activitat que es presenta té les següents característiques, totes elles rellevants: La poden realitzar alhora tots els alumnes. És una activitat inclusiva, no necessita de grans coneixements previs per part de l’alumnat i poden treballar conjuntament alumnes de diferents nivells. Tots aporten al resultat final.Té un fort component artístic que, sense moltes dificultats, permetrà que els resultats llueixin en el centre.De seguida i de forma natural, portarà els alumnes a investigar sobre les característiques dels políedres, així com els seus elements: arestes, vèrtexs, cares, angles, díedres, etc.Es pot realitzar a qualsevol curs de l’ESO, per tant, és una bona activitat intercursos o internivells.És una activitat de llarg recorregut: en funció de l’alumne es pot estirar més i, fins i tot pot esdevenir un projecte de recerca.Té un cost molt baix i demana de la implicació de tots per tal de realitzar-se.
The Bridges Organization - The Bridges Organization. 2019 Bridges Conference. The Bridges Archive: 2019. We are in the National Museum of Mathematics in New York! Experience Workshop and GeoGebra join forces to show the power of STEAM – Experience Workshop. It’s GeoGebra Day at MoMath!

Saturday, March 30 Special guest of the event is the renowned artist, architect, designer and symmetrologist, Haresh Lalvani, who will demonstrate his tessellation system, Pentiles together with Experience Workshop‘s STEAM coordinator, Kristóf Fenyvesi. Don’t miss this one-day opportunity to meet and learn from the creators of GeoGebra! Learn how to use GeoGebra’s free online math tools to build and test your own 3D models or to transform your photo into augmented reality. Enhance the student learning experience with digital tools to explore mathematical concepts in areas such as algebra, precalculus, and trigonometry.
Register here: GeoGebra Day at MoMath “For Educators: Using GeoGebra to Create Active & Engaging Learning Environments” with Tim Brzezinski and Steve Phelps 10:00 to 11:30 amEducators, foster active student discovery in your classroom! Les trames géométriques et sonores de l'univers. Aspects géométriques et sonores de l'univers Alain Boudet Dr en Sciences Physiques Résumé: Loin d'être dues au hasard, les formes de l'univers sont sous-tendues par des trames géométriques.

On constate leur présence depuis l'atome jusqu'aux amas de galaxies, en passant par les plantes, les animaux, les circuits énergétiques de la Terre, et même le corps humain. Ces géométries sont intimement liées à des fréquences sonores. Contenu de l'article Annexe Les scientifiques nous affirment que l'univers est né à partir d'un point microscopique qui a explosé dans un immense Big Bang.
Dans cette évolution, ce qui aurait présidé à l'apparition des magnifiques formes de la matière et de la vie, c'est le plus pur des hasards. Ce scénario n'est pas la transcription d'observations directes. Les astrophysiciens adhèrent massivement à cette théorie. Le but de cette étude n'est pas de polémiquer sur l'opposition entre la théorie scientifique cosmologique actuelle et le créationnisme. Polyèdres. Icosaedro áureo - Divermates Blog. ¿Sabías que en el interior del icosaedro se intersecan tres rectángulos iguales?
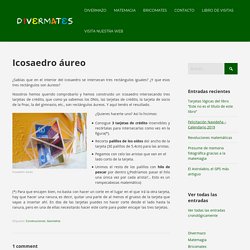
¿Y que esos tres rectángulos son áureos? Nosotros hemos querido comprobarlo y hemos construido un icosaedro intersecando tres tarjetas de crédito, que como ya sabemos los DNIs, las tarjetas de crédito, la tarjeta de socio de la Fnac, la del gimnasio, etc., son rectángulos áureos. Y aquí tenéis el resultado. Icosaedro áureo ¿Quieres hacerte uno? Consigue 3 tarjetas de crédito inservibles y recórtalas para intersecarlas como ves en la figura(*).Recorta palillos de los oídos del ancho de la tarjeta (30 palillos de 5.4cm) para las aristas.Pegamos con celo las aristas que van en el lado corto de la tarjeta.Unimos el resto de los palillos con hilo de pescar por dentro (¿Podríamos pasar el hilo una única vez por cada arista?
Using Islamic Geometry for Student Buy-In. Written by: Dr.

Christine von Renesse and Dr. Philip DeOrsey. In this blog we describe an activity that is especially helpful in getting student buy-in. You can read our blog about student resistance and student buy-in to learn more about models and research on this topic. Make your own Kaleidocycles! Images des mathématiques. Piste bleue Le 6 février 2013 - Ecrit par Étienne Ghys, Jos Leys Lire l'article en Vous vous souvenez du théorème de Pythagore ?
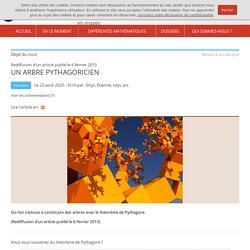
Le carré de l’hypoténuseEst égal, si je ne m’abuseÀ la somme des carrésConstruits sur les autres côtés [1]. Partons d’un triangle rectangle très spécial puisqu’il est aussi isocèle. Le théorème de Pythagore dit précisément que l’aire du grand carré bleu est égale à la somme des aires des deux petits carrés. La géométrie autour de nous. Qu’on aime ou qu’on n’aime pas, on vit avec.
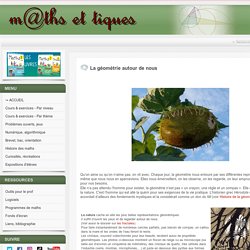
Chaque jour, la géométrie nous entoure par ses différentes représentations sans même que nous nous en apercevions. Elles nous émerveillent, on les observe, on les regarde, on leur emprunte leurs propriétés pour nos besoins.Elle n’a pas attendu l’homme pour exister, la géométrie n’est pas « un crayon, une règle et un compas ». Elle est nature et dans la nature. C'est l’homme qui est allé la quérir pour ses exigences de la vie pratique. L’historien grec Hérodote (-484 ; -425) lui accordait d’ailleurs des fondements mystiques et la considérait comme un don du Nil (voir Histoire de la géométrie). Le monde animal et le monde végétal offrent également de nombreux exemples. Il existe bien d’autres similitudes comme par exemple l’œil de mouche (vu au microscope) et le nid de guêpes tous deux formés de petits hexagones. Même dans l’homme, Leonard de Vinci a trouvé une organisation géométrique.