

Image maps1. Heterocedasticidad. Definición[editar] En estadística se dice que un modelo de regresión lineal presenta heterocedasticidad cuando la varianza de los errores no es constante en todas las observaciones realizadas.
Esto implica el incumplimiento de una de las hipótesis básicas sobre las que se asienta el modelo de regresión lineal. De ella se deriva que los datos con los que se trabaja son heterogéneos, ya que provienen de distribuciones de probabilidad con distinta varianza. Regresión lineal. En estadística la regresión lineal o ajuste lineal es un modelo matemático usado para aproximar la relación de dependencia entre una variable dependiente Y, las variables independientes Xi y un término aleatorio ε.
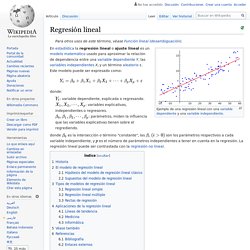
Este modelo puede ser expresado como: donde: : variable dependiente, explicada o regresando. Estadística. La estadística (la forma femenina del término alemán Statistik, derivado a su vez del italiano statista, "hombre de Estado"),[1] es la rama de las matemáticas que estudia la variabilidad, así como el proceso aleatorio que la genera siguiendo leyes de probabilidad.[2] Como parte de la matemática, la estadística es una ciencia formal deductiva, con un conocimiento propio, dinámico y en continuo desarrollo obtenido a través del método científico formal.
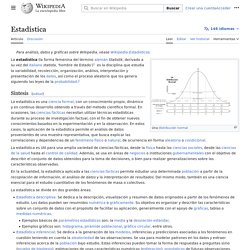
En ocasiones, las ciencias fácticas necesitan utilizar técnicas estadísticas durante su proceso de investigación factual, con el fin de obtener nuevos conocimientos basados en la experimentación y en la observación. En estos casos, la aplicación de la estadística permite el análisis de datos provenientes de una muestra representativa, que busca explicar las correlaciones y dependencias de un fenómeno físico o natural, de ocurrencia en forma aleatoria o condicional. La estadística se divide en dos grandes áreas: Historia[editar] dado. Variance function. In statistics, the variance function is a smooth function which depicts the variance of a random quantity as a function of its mean.
Estimador. En estadística, un estimador es un estadístico (esto es, una función de la muestra) usado para estimar un parámetro desconocido de la población.
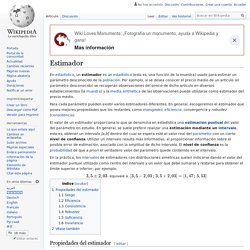
Por ejemplo, si se desea conocer el precio medio de un artículo (el parámetro desconocido) se recogerán observaciones del precio de dicho artículo en diversos establecimientos (la muestra) y la media aritmética de las observaciones puede utilizarse como estimador del precio medio. El valor de un estimador proporciona lo que se denomina en estadística una estimación puntual del valor del parámetro en estudio. En general, se suele preferir realizar una estimación mediante un intervalo, esto es, obtener un intervalo [a,b] dentro del cual se espera esté el valor real del parámetro con un cierto nivel de confianza. Utilizar un intervalo resulta más informativo, al proporcionar información sobre el posible error de estimación, asociado con la amplitud de dicho intervalo. Equivale a. Omnibus test. In addition, Omnibus test as a general name refers to an overall or a global test.
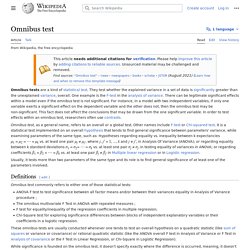
Other names include F-test or Chi-squared test. Omnibus test as a statistical test is implemented on an overall hypothesis that tends to find general significance between parameters' variance, while examining parameters of the same type, such as: Hypotheses regarding equality vs. inequality between k expectancies μ1=μ2=... =μk vs. at least one pair μj≠μj' , where j,j'=1,... Prueba de Goldfeld–Quandt. En estadística, el test de Goldfeld-Quandt (por Stephen Goldfeld y Richard E.
Quandt) comprueba la homocedasticidad en análisis de regresión. Para ello divide un conjunto de datos en dos partes o grupos, y por lo tanto la prueba a veces se llama una prueba de dos grupos. La prueba Goldfeld-Quandt es uno de dos pruebas propuestas en un artículo de 1965 por Stephen Goldfeld y Richard Quandt. Tanto el método paramétrico como no paramétrico se describen en el documento, pero el término "prueba Goldfeld-Quandt" por lo general se asocian únicamente con el primero. Mínimos cuadrados generalizados. En estadística, los mínimos cuadrados generalizados (en inglés, generalized least squares (GLS)) es una técnica para la estimación de los parámetros desconocidos en un modelo de regresión lineal.
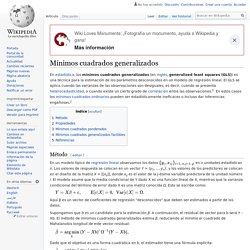
Prueba de Park. Regresión logística. En estadística, la regresión logística es un tipo de análisis de regresión utilizado para predecir el resultado de una variable categórica (una variable que puede adoptar un número limitado de categorías) en función de las variables independientes o predictoras.
Es útil para modelar la probabilidad de un evento ocurriendo como función de otros factores. El análisis de regresión logística se enmarca en el conjunto de Modelos Lineales Generalizados (GLM por sus siglas en inglés) que usa como función de enlace la función logit. Las probabilidades que describen el posible resultado de un único ensayo se modelan, como una función de variables explicativas, utilizando una función logística. La regresión logística es usada extensamente en las ciencias médicas y sociales. Otros nombres para regresión logística usados en varias áreas de aplicación incluyen modelo logístico, modelo logit, y clasificador de máxima entropía. Prueba F de Fisher. En estadística se denomina prueba F de Snedecor a cualquier prueba en la que el estadístico utilizado sigue una distribución F si la hipótesis nula no puede ser rechazada.
El nombre fue acuñado en honor a Ronald Fisher. La hipótesis de que las medias de múltiples poblaciones normalmente distribuidas y con la misma desviación estándar son iguales. Esta es, quizás, la más conocida de las hipótesis verificada mediante el test F y el problema más simple del análisis de varianza.La hipótesis de que las desviaciones estándar de dos poblaciones normalmente distribuidas son iguales, lo cual se cumple. Distribución normal. En estadística y probabilidad se llama distribución normal, distribución de Gauss, distribución gaussiana o distribución de Laplace-Gauss, a una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece en estadística y en la teoría de probabilidades.[1] La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico.
Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana.[2] La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos. [3]Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes. Máxima verosimilitud. En estadística, la estimación por máxima verosimilitud (conocida también como EMV y, en ocasiones, MLE por sus siglas en inglés) es un método habitual para ajustar un modelo y estimar sus parámetros. Historia[editar] Fue recomendado, analizado y popularizado por R. A. Fisher entre 1912 y 1922, aunque había sido utilizado antes por Carl Friedrich Gauss, Pierre-Simon Laplace, Thorvald N. Thiele y Francis Edgeworth.[1] Distribución normal multivariante.
En probabilidad y estadística, una distribución normal multivariante, también llamada distribución gaussiana multivariante, es una generalización de la distribución normal unidimensional a dimensiones superiores. Prueba t de Student. En estadística, una prueba t de Student, prueba t de estudiante, o Test-T es cualquier prueba en la que el estadístico utilizado tiene una distribución t de Student si la hipótesis nula es cierta.
Se aplica cuando la población estudiada sigue una distribución normal pero el tamaño muestral es demasiado pequeño como para que el estadístico en el que está basada la inferencia esté normalmente distribuido, utilizándose una estimación de la desviación típica en lugar del valor real. Es utilizado en análisis discriminante. Historia[editar] El estadístico t fue introducido por William Sealy Gosset en 1908, un químico que trabajaba para la cervecería Guinness de Dublín. Usos[editar] Mínimos cuadrados. El resultado del ajuste de un conjunto de datos a una función cuadrática. Mínimos cuadrados es una técnica de análisis numérico enmarcada dentro de la optimización matemática, en la que, dados un conjunto de pares ordenados —variable independiente, variable dependiente— y una familia de funciones, se intenta encontrar la función continua, dentro de dicha familia, que mejor se aproxime a los datos (un "mejor ajuste"), de acuerdo con el criterio de mínimo error cuadrático.
En su forma más simple, intenta minimizar la suma de cuadrados de las diferencias en las ordenadas (llamadas residuos) entre los puntos generados por la función elegida y los correspondientes valores en los datos. Específicamente, se llama mínimos cuadrados promedio (LMS) cuando el número de datos medidos es 1 y se usa el método de descenso por gradiente para minimizar el residuo cuadrado. Mínimos cuadrados ordinarios. En estadística, los mínimos cuadrados ordinarios (MCO) o mínimos cuadrados lineales es el nombre de un método para encontrar los parámetros poblacionales en un modelo de regresión lineal. Este método minimiza la suma de las distancias verticales entre las respuestas observadas en la muestra y las respuestas del modelo.
El parámetro resultante puede expresarse a través de una fórmula sencilla, especialmente en el caso de un único regresionador. El método MCO, siempre y cuando se cumplan los supuestos clave, será consistente cuando los regresionadores sean exógenos y no haya perfecta multicolinealidad, este será óptimo en la clase de parámetros lineales cuando los errores sean homocedásticos y además no haya autocorrelación.
En estas condiciones, el método de MCO proporciona un estimador insesgado de varianza mínima siempre que los errores tengan varianzas finitas. Bajo la suposición adicional de que los errores se distribuyen normalmente, el estimador MCO es el de máxima verosimilitud. Test de Breusch-Pagan. En estadística, el test de Breusch-Pagan se utiliza para determinar la heterocedasticidad en un modelo de regresión lineal. Analiza si la varianza estimada de los residuos de una regresión dependen de los valores de las variables independientes.
Dummy variable (statistics) Figure 1 : Graph showing wage = α0 + δ0female + α1education + U, δ0 < 0. Dummy variables are incorporated in the same way as quantitative variables are included (as explanatory variables) in regression models. For example, if we consider a Mincer-type regression model of wage determination, wherein wages are dependent on gender (qualitative) and years of education (quantitative): where. Regression diagnostic. In statistics, a regression diagnostic is one of a set of procedures available for regression analysis that seek to assess the validity of a model in any of a number of different ways.[1] This assessment may be an exploration of the model's underlying statistical assumptions, an examination of the structure of the model by considering formulations that have fewer, more or different explanatory variables, or a study of subgroups of observations, looking for those that are either poorly represented by the model (outliers) or that have a relatively large effect on the regression model's predictions.
A regression diagnostic may take the form of a graphical result, informal quantitative results or a formal statistical hypothesis test,[2] each of which provides guidance for further stages of a regression analysis. Estimación de la desviación estándar no sesgada. Varianza. Distribución beta. En estadística la distribución beta es una distribución de probabilidad continua con dos parámetros y.