Igor et Grichka Bogdanoff. Cet article ou cette section traite d’une personne morte récemment (28 décembre 2021). Le texte peut changer fréquemment, n’est peut-être pas à jour et peut manquer de recul. N’hésitez pas à participer, en veillant à citer vos sources. Les biographies étant habituellement écrites au présent de narration, merci de ne pas mettre au passé les verbes qui sont actuellement au présent. L'emploi des mots « mort » et « décès » est discuté sur cette page.La dernière modification de cette page a été faite le 28 décembre 2021 à 22:29. Igor et Grichka Bogdanoff Grichka et Igor Bogdanoff en 2016. La valeur scientifique de leurs travaux de thèse a été sérieusement mise à mal par une grande partie de la communauté scientifique, ainsi que leur manière de vulgariser la science.
Biographie Famille Igor Bogdanoff Igor Bogdanoff est père de six enfants, de trois femmes différentes[9]. Grichka Bogdanoff Grichka Bogdanoff est resté célibataire et n'a jamais eu d'enfants[17]. Enfance et débuts Contribution scientifique. L’origine et l’avenir du monde… | Igor & Grichka BOGDANOV. Théorème de complétude de Gödel. La formule En logique mathématique, le théorème de complétude du calcul des prédicats du premier ordre[1] dresse une correspondance entre la sémantique[2] et les démonstrations d'un système de déduction en logique du premier ordre. 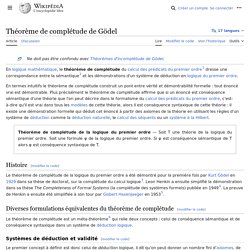En termes intuitifs le théorème de complétude construit un pont entre vérité et démontrabilité formelle : tout énoncé vrai est démontrable. Plus précisément le théorème de complétude affirme que si un énoncé est conséquence sémantique d'une théorie que l'on peut décrire dans le formalisme du calcul des prédicats du premier ordre, c'est-à-dire qu'il est vrai dans tous les modèles de cette théorie, alors il est conséquence syntaxique de cette théorie : il existe une démonstration formelle qui dérive cet énoncé à partir des axiomes de la théorie en utilisant les règles d'un système de déduction comme la déduction naturelle, le calcul des séquents ou un système à la Hilbert.
Histoire[modifier | modifier le code] Quelques définitions[modifier | modifier le code] Théorèmes d'incomplétude de Gödel. Les théorèmes d'incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, publiés par Kurt Gödel en 1931 dans son article Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme (en) (« Sur les propositions formellement indécidables des Principia Mathematica et des systèmes apparentés »). Ils ont marqué un tournant dans l'histoire de la logique en apportant une réponse négative à la question de la démonstration de la cohérence des mathématiques posée plus de 20 ans auparavant par le programme de Hilbert.
Le second théorème d'incomplétude est à la fois un corollaire et une formalisation d'une partie de la preuve du premier. Énoncés des deux théorèmes[modifier | modifier le code] Le premier théorème d'incomplétude peut être énoncé de la façon encore un peu approximative suivante (les termes techniques sont expliqués dans le paragraphe suivant). De tels énoncés sont dits indécidables dans cette théorie. On dit également indépendants de la théorie. Le théorème d’incomplétude de Gödel. C’est en cours de philo que j’en ai entendu parler pour la première fois !
Notre prof nous faisait un cours sur la logique et ses fondements, et c’est alors qu’elle le mentionna : le fameux théorème de Gödel, celui qui prouve que quoi qu’on fasse, il existe des énoncés mathématiques vrais, mais indémontrables. Les mathématiques resteront à tout jamais un édifice imparfait ! J’en fus évidemment tout retourné et fasciné : comment était-il possible qu’un truc pareil existe ? Comment prouver ce résultat pouvait même être du domaine de la science ? Peut-on tout démontrer en mathématiques ? Quand on fait des mathématiques, on manipule des énoncés.
Un énoncé est une suite de symboles ou une phrase ayant un sens mathématique précis. Quand on considère un énoncé mathématique, on ne sait pas forcément à l’avance s’il est vrai ou faux. Si un mathématicien arrive à démontrer un énoncé, on considère que cet énoncé est « vrai ». A quoi jouent les mathématiciens ? Ce que dit le théorème de Gödel. Preview: How the Fourier Transform Works: Lecture #4 - Euler's Identity (Full Video)
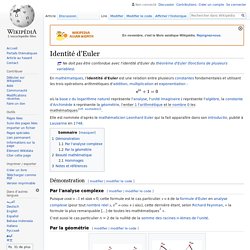
The God equation Euler's Identity. Identité d'Euler. Un article de Wikipédia, l'encyclopédie libre. En mathématiques, l'identité d'Euler est une relation entre plusieurs constantes fondamentales et utilisant les trois opérations arithmétiques d'addition, multiplication et exponentiation : Elle est nommée d'après le mathématicien Leonhard Euler qui la fait apparaître dans son Introductio, publié à Lausanne en 1748. Démonstration[modifier | modifier le code] Par l'analyse complexe[modifier | modifier le code] Puisque cosπ = –1 et sinπ = 0, cette formule est le cas particulier x = π de la formule d'Euler en analyse complexe (pour tout nombre réel x, eix = cosx + i sinx), cette dernière étant, selon Richard Feynman, « la formule la plus remarquable […] de toutes les mathématiques[2] ».
C'est aussi le cas particulier n = 2 de la nullité de la somme des racines n-ièmes de l'unité. Par la géométrie[modifier | modifier le code] Juxtaposition de 8 triangles rectanglesJuxtaposition de 16 triangles rectangles Beauté mathématique[modifier | modifier le code]