

Qinwf/awesome-R. Regression Analysis Tutorial and Examples. I’ve written a number of blog posts about regression analysis and I think it’s helpful to collect them in this post to create a regression tutorial.
I’ll supplement my own posts with some from my colleagues. This tutorial covers many aspects of regression analysis including: choosing the type of regression analysis to use, specifying the model, interpreting the results, determining how well the model fits, making predictions, and checking the assumptions. At the end, I include examples of different types of regression analyses. If you’re learning regression analysis right now, you might want to bookmark this tutorial! How to Interpret a Regression Model with Low R-squared and Low P values. In regression analysis, you'd like your regression model to have significant variables and to produce a high R-squared value.
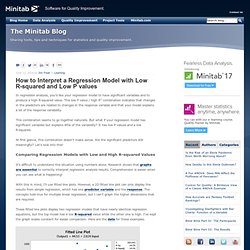
This low P value / high R2 combination indicates that changes in the predictors are related to changes in the response variable and that your model explains a lot of the response variability. This combination seems to go together naturally. But what if your regression model has significant variables but explains little of the variability? It has low P values and a low R-squared. At first glance, this combination doesn’t make sense. Comparing Regression Models with Low and High R-squared Values It’s difficult to understand this situation using numbers alone.
With this in mind, I'll use fitted line plots. These fitted line plots display two regression models that have nearly identical regression equations, but the top model has a low R-squared value while the other one is high. List of current heads of state and government. This is a list of current heads of state and government, showing heads of state and heads of government where different, mainly in parliamentary systems; often a leader is both in presidential systems.
Some states have semi-presidential systems where the head of government role is fulfilled by both the listed head of government and the head of state. Some things R can do you might not be aware of. There is a lot of noise around the "R versus Contender X" for Data Science.

I think the two main competitors right now that I hear about are Python and Julia. I'm not going to weigh into the debates because I go by the motto: "Why not just use something that works? " R offers a lot of benefits if you are interested in statistical or predictive modeling. It is basically unrivaled in terms of the breadth of packages for applied statistics. But I think sometimes it isn't obvious that R can handle some tasks that you used to have to do with other languages. Entropy (information theory) 2 bits of entropy.
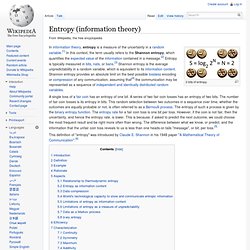
A single toss of a fair coin has an entropy of one bit. A series of two fair coin tosses has an entropy of two bits. The number of fair coin tosses is its entropy in bits. This random selection between two outcomes in a sequence over time, whether the outcomes are equally probable or not, is often referred to as a Bernoulli process. Entropy (information theory) Maximum likelihood. In statistics, maximum-likelihood estimation (MLE) is a method of estimating the parameters of a statistical model.

When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters. The method of maximum likelihood corresponds to many well-known estimation methods in statistics. For example, one may be interested in the heights of adult female penguins, but be unable to measure the height of every single penguin in a population due to cost or time constraints. Assuming that the heights are normally (Gaussian) distributed with some unknown mean and variance, the mean and variance can be estimated with MLE while only knowing the heights of some sample of the overall population.
MLE would accomplish this by taking the mean and variance as parameters and finding particular parametric values that make the observed results the most probable (given the model). Principles[edit] Note that the vertical bar in . Where . . Probability distribution. Estimator. In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result (the estimate) are distinguished.
There are point and interval estimators. The point estimators yield single-valued results, although this includes the possibility of single vector-valued results and results that can be expressed as a single function. This is in contrast to an interval estimator, where the result would be a range of plausible values (or vectors or functions). Statistical theory is concerned with the properties of estimators; that is, with defining properties that can be used to compare different estimators (different rules for creating estimates) for the same quantity, based on the same data.
Such properties can be used to determine the best rules to use under given circumstances. Background[edit] . List of probability distributions. Many probability distributions are so important in theory or applications that they have been given specific names.
Discrete distributions[edit] With finite support[edit] With infinite support[edit] Continuous distributions[edit] Supported on a bounded interval[edit] Supported on semi-infinite intervals, usually [0,∞)[edit]