

Ballistic Trajectory (2-D) Calculator - Computes the maximum height, range, time to impact, and impact velocity of a ballistic projectile. The motion of an object moving near the surface of the earth can be described using the equations: (1): x = xo + vxo·t (2): y = yo + vyo·t - 0.5·g·t2 The calculator solves these two simultaneous equations to obtain a description of the ballistic trajectory.
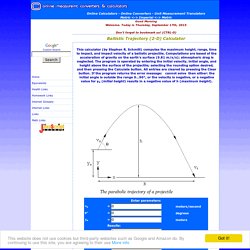
The horizontal and vertical components of initial velocity are determined from: vxo = vo·cos θ vyo = vo·sin θ Then the calculator computes the time to reach the maximum height by finding the time at which vertical velocity becomes zero: vy = vyo - g·t trise = vyo/g Maximum height is obtained by substitution of this time into equation (2). h = yo + vyo·t - 0.5·g·t2 Next, the time to fall from the maximum height is computed by solving equation (2) for an object dropped from the maximum height with zero initial velocity. 0 = h - 0.5·g·t2 tfall = √(2·h/g) Games 2D. CannonTrajectory. Contents Description of CannonTrajectory The unit called CannonTrajectory implements the Java program for computing the trajectory of a cannonball or other projectile fired from the surface of the Earth, at an arbitrary angle and speed.

Users can experiment to see what angle gives the greatest range. This program is the most elementary one in the book, and many later programs are based on it.It is introduced in Investigation 1.3. It introduces the important programming concept of loops. Using CannonTrajectory If you have not used Triana before, read the instructions first. Initially this window will not necessarily use the same scale for distances in the horizontal and vertical direction, since it is set by default to adjust the scales to show the most information about the curve.
You can change the initial speed, angle, and time-step by using the parameter window of the unit, illustrated here. Understanding CannonTrajectory Loops are described in the Introduction to Programming in Java. Another Cannonball - Jared Nelson - Java for Video Games. View Another Cannonball Source Code:View Another Cannonball Javadoc Description: A Java program that implements a Cannonball class, which simulates a cannonball that shoots into the air at an angle and is affected by gravity, and displays the position of the cannonball every second until the cannonball hits the ground.

How solution works: First I designed the Cannonball class, which was very similar to the Cannonball class from Exercise P7.3. However, this cannonball class contains instance fields for the location of the cannonball relative to its starting position (in meters) and the x- and y-velocity of the cannonball (meters/second), a constructor that positions the cannonball at the point (0, 0) with the specified velocity magnitude (in meters/second) and angle (in radians), and methods to update the position and velocity of the cannonball with the amount of time passed as well as to return the position of the cannonball.
Development: Android. Trigonometry for Game Programming: Part 1/2. Learn Trigonometry for game programming!
This is a post by iOS Tutorial Team member Matthijs Hollemans, an experienced iOS developer and designer. You can find him on Google+ and Twitter. Does the thought of doing mathematics give you cold sweats? Are you ready to give up on your career as a budding game developer because the math just doesn’t make any sense to you?
Don’t fret – math can be fun, and this cool 2-part game tutorial will back up that claim! Here’s a little secret: as an app developer, you don’t really need to know a lot of math. That said, for making games it is useful to have a few more math skills in your toolbox. In this tutorial, you will learn about some important trigonometric functions and how you can use them in your games. Don’t worry if you’ve never used Cocos2D before or are going to use a different framework for your game – the mathematics we’ll cover in this tutorial will apply to your engine no matter what.
Getting Started: It’s All About Triangles a2 + b2 = c2. Coding Destructible Pixel Terrain: How to Make Everything Explode.
Unity.