

01 arithmetique introduction 01. Chapitre 10 Arithmétique divisibilite nb premiers. Exos livrescolaire p 29. Discord jeudi 9 Avril 2020. Discord jeudi 30 Avril 2020. Discord le jeudi 7 Mai 2020. Cor exos arithmétique. Francoise-jadot/exo113p29.py — Python — NumWorks Workshop. Seconde (méthode) : "Montrer qu'un nombre est un diviseur/multiple d'un autre nombre" 09 arithmetique definition PGCD exemple 01. 14 arithmetique algorithme euclide 01. 16 arithmetique PGCD euclide. 17 arithmetique nombres premiers entre eux 01. 21 arithmetique fraction irreductible methode. PGCD. PPCM PGCD appli fractions. A quelle heure verra-t-on à nouveau les tramways? Simplification de racines. Module test primalité livresco p 31. Aide pour le 3 du 131 p 32. POUR LES GOURMANDS: DM facultatif pour le lundi 27 Avril 2020. Correction du DM POUR LES GOURMANDS. Trois divise six. Trois ne divise pas cinq. N divise m.
468 en facteurs premiers avec la Numworks. Sauras-tu trouver ce nombre ? Les nombres premiers — Science étonnante #34. EPISODE 03 - Les nombres premiers. Les Nombres PREMIERS - Cours + Exercices. Savoir si un nombre est premier. ♕ savoir si un nombre est premier - Technique très efficace - exemple avec 199 - seconde. Nombres premiers. Tout nombre non nul possède évidemment deux diviseurs : 1 et lui-même.
Il advient que dans le cas de l'unité ces deux diviseurs évidents se confondent. Or certains nombres ne possèdent pas d'autres diviseurs que ces deux diviseurs 'triviaux', on les appelle les nombres 'premiers' , c'est par exemple le cas de 2, 3, 5, etc... Les raisons pour lesquelles on refuse à 1 la qualité de nombre premier ne tiennent pas au fait que c'est le neutre de la multiplication mais plutôt au fait que c'est le seul élément inversible de ℕ.
Il résulte de la théorie des anneaux que les éléments inversibles n'ont pas à être pris en compte pour les problèmes de décomposition (factorisation), faute de quoi on ne peut énoncer correctement les théorèmes. On retiendra donc simplement pour le moment que 1 n'est pas premier et qu'on peut prendre pour définition des nombres naturels premiers: Nombres premiers Kentzel. Nombres premiers. Nombres premiers est un outil pour les recherches de nombres premiers.
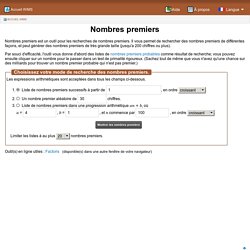
Il vous permet de rechercher des nombres premiers de différentes façons, et peut générer des nombres premiers de très grande taille (jusqu'a 200 chiffres ou plus). Par souci d'efficacité, l'outil vous donne d'abord des listes de nombres premiers probables comme résultat de recherche; vous pouvez ensuite cliquer sur un nombre pour le passer dans un test de primalité rigoureux.
(Sachez tout de même que vous n'avez qu'une chance sur des milliards pour trouver un nombre premier probable qui n'est pas premier.) Outil(s) en ligne utiles : Factoris (disponible(s) dans une autre fenêtre de votre navigateur) Nombres premiers -aide en ligne maths-videos - Seconde.
Divisibilité - nombrespremiers -2nde- Nombres divisibles par 3 ou 9. Les nombres divisibles par 2, 3, 4 jusqu'à 11. Par Clément (9 ans) – Août 2011 Découverte Junior – Gérard Villemin NOMBRES DIVISIBLES PAR 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ou 11 Comment savoir rapidement si un nombre est divisible par un autre.
Exercice pour savoir les utiliser. 182. 3ème Olympique-Critère de divisibilité par 7. CALCUL MENTAL'Ô ! : Le critère de divisibilité par 7 de Chika Ofili. Critère de divisibilité par 7. Les critères de divisibilité. Les critères de divisibilité□ Les règles de divisibilité - ppt video online télécharger. Diviseurs ou pas diviseurs ** Reconnaitre multiple & diviseur.
06 Divisibilité et Python. Divisibilité. Cours [Seconde] - Multiples, diviseurs et nombres premiers. Divisibilité - nombrespremiers -2nde- Décomposition en produit de facteurs premiers. Decomposition en facteurs premiers. Voici un des résultats les plus importants de l'arithmétique: Tout nombre n≥2 se décompose en produit de facteurs premiers.
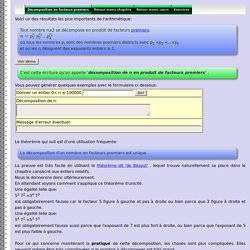
Où tous les nombres pi sont des nombres premiers distincts avec p12 <...k et où les ri désignent des exposants entiers ≥ 1. La preuve constitue un excellent cas de récurrence forte. Le théorème est vrai pour 2. Soit n un entier n >2 si n est premier il n'y a rien à démontrer. C'est cette écriture qu'on appelle 'décomposition de n en produit de facteurs premiers' . Vous pouvez générer quelques exemples avec le formulaire ci-dessous: Le théorème qui suit est d'une utilisation fréquente: La décomposition d'un nombre en facteurs premiers est unique. La preuve est très facile en utilisant le théorème dit 'de Bézout' , lequel trouve naturellement sa place dans le chapitre consacré aux entiers relatifs. Pour ce qui concerne maintenant la pratique de cette décomposition, les choses sont plus compliquées.
Café Python. Décomposer 550 ; 320 ; 1000 en produit de facteurs premiers. Décomposition d'un entier naturel en produit de facteurs premiers Python. Nombres et calcul - Multiples, diviseurs et nombres premiers. Multiples et diviseurs. Multiples. Le plus petit commun multiple (PPCM) Plus petit commun multiple. Définitions Toutes les propositions enoncées ici seront démontrées ultérieurement dans le chapitre consacré aux entiers relatifs.
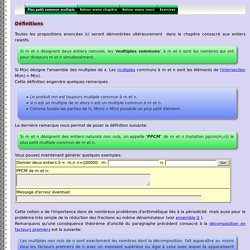
Si m et n désignent deux entiers naturels, les 'multiples communs' à m et n sont les nombres qui ont pour diviseurs m et n simultanément. Si M(x) désigne l'ensemble des multiples de x. Le plus grand commun diviseur (PGCD) Plus grand commun diviseur. Définitions Toutes les propositions enoncées ici seront démontrées ultérieurement dans le chapitre consacré aux entiers relatifs.
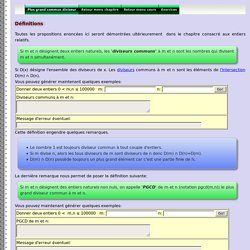
Nombres premiers, PGCD, PPCM Notes de cours MAFIADOC. PGCD, PPCM EXERCICES CORRIGES MAFIADOC. Algorithme d'Euclide. Fonction pgdc(a,b) avec NumWorks. Plus grand multiple. PGCD algorithme illustré via Algobox.
Nombres premiers entre eux. Définition Deux nombres entiers naturels m et n sont dits 'premiers entre eux' si leur PGCD est égal à 1.
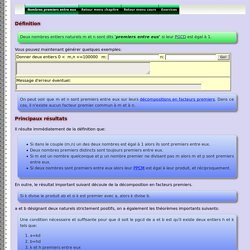
Vous pouvez maintenant générer quelques exemples: Principaux résultats Il résulte immédiatement de la définition que: Arithmétique cours 2. [AVENT MATHS] : 9 est une preuve ? Problème de Flavius Josèphe à programmer en Python :) Grilles binaires. Les nombres pilpoils (Lycée Kastler Denain) LE COURS : Arithmétique - Troisième. Arithmétique. Jnicaud. Un jeune nigérian de 12 ans dévoile une propriété de maths. Le calcul de Sofiane. Maths 2019- Cours 2nde - Arithmétique dans N. La somme de deux multiples de a est un multiple de a. Mathématiques - algorithme et programmation - nombres et calculs. Espace pédagogique > disciplines du second degré > mathématiques > enseignement > activités pédagogiques mis à jour le 15/05/2019 Des exemples pour l'agorithmique et la programmation en 2nde. mots clés : algorithmique, nombre, calcul L’utilisation de logiciels (calculatrice ou ordinateur), d’outils de visualisation et de représentation, de calcul (numérique ou formel), de simulation, de programmation développe la possibilité d’expérimenter, ouvre largement le dialogue entre l’observation et la démonstration et change profondément la nature de l’enseignement .
L’algorithmique a une place naturelle dans tous les champs des mathématiques et les problèmes ainsi traités doivent être en relation avec les autres parties du programme (fonctions, géométrie, statistiques et probabilité, logique) mais aussi avec les autres disciplines ou la vie courante. Nombre et calculs.
Nombres Relatifs (Multiplication et Division) Activite connecteurs groupe logique. Lois de De Morgan. Un article de Wikipédia, l'encyclopédie libre.
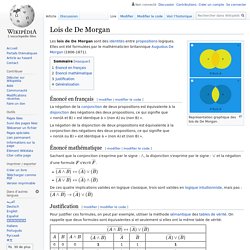
Représentation graphique des lois de De Morgan. Énoncé en français[modifier | modifier le code] La négation de la conjonction de deux propositions est équivalente à la disjonction des négations des deux propositions, ce qui signifie que « non(A et B) » est identique à « (non A) ou (non B) ». La négation de la disjonction de deux propositions est équivalente à la conjonction des négations des deux propositions, ce qui signifie que « non(A ou B) » est identique à « (non A) et (non B) ». Énoncé mathématique[modifier | modifier le code] Sachant que la conjonction s'exprime par le signe : , la disjonction s'exprime par le signe : et la négation d'une formule. 2ndeArithm. 23.3e-Vélos et fractions. 8PY9.1 : p.29 - im.51. Mathématiques - Curiosités arithmétiques. Pour la deuxième situation, les élèves ont d'abord mobilisé un tableur pour constater qu'effectivement, le nombre s'écrit sous la forme du carré d'un nombre entier N mais ils ont du mal à exprimer cet entier N en fonction de n.
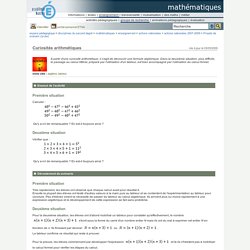
Ils finissent par deviner ou .Le tableur confirme ce résultat qui reste à prouver. Exercices sur les ensembles de nombres - Algorithmique. Sauras-tu trouver la logique de ces 2 séries de nombres ? POURQUOI LE PREMIER NOMBRE N’EST PAS UN NOMBRE PREMIER. Les nombres premiers ont fasciné et fascinent toujours un nombre incalculable de gens, qu’ils soient ou non mathématiciens de profession. Cette passion a engendré pléthore de théorèmes les concernant, dont certains sont d’une sophistication hallucinante. Parmi ces théorèmes, y en a-t-il de plus importants que d’autres ?
Cela dépend du point de vue, mais ce qui est sûr, c’est que la complexité du monde des nombres premiers provient du théorème suivant, déjà connu d’Euclide : Théorème : Il existe une infinité de nombres premiers. Ce théorème a une preuve très courte !