

19 juin - Le système RSA. Chiffrement RSA (page Wikipedia) Le chiffrement RSA (nommé par les initiales de ses trois inventeurs) est un algorithme de cryptographie asymétrique, très utilisé dans le commerce électronique, et plus généralement pour échanger des données confidentielles sur Internet.
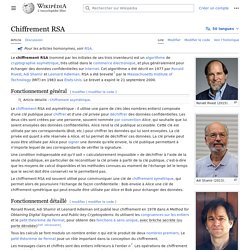
Cet algorithme a été décrit en 1977 par Ronald Rivest, Adi Shamir et Leonard Adleman. RSA a été breveté[1] par le Massachusetts Institute of Technology (MIT) en 1983 aux États-Unis. Le brevet a expiré le 21 septembre 2000. Fonctionnement général[modifier | modifier le code] Le chiffrement RSA est asymétrique : il utilise une paire de clés (des nombres entiers) composée d'une clé publique pour chiffrer et d'une clé privée pour déchiffrer des données confidentielles. Le chiffrement RSA est souvent utilisé pour communiquer une clé de chiffrement symétrique, qui permet alors de poursuivre l'échange de façon confidentielle : Bob envoie à Alice une clé de chiffrement symétrique qui peut ensuite être utilisée par Alice et Bob pour échanger des données.
12 juin - Le petit théorème de Fermat et les nombres de Carmichaël - A lire. Le petit théorème de Fermat (page Wikipedia) En mathématiques, le petit théorème de Fermat est un résultat de l'arithmétique modulaire, qui peut aussi se démontrer avec les outils de l'arithmétique élémentaire.
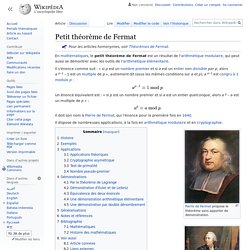
Un énoncé équivalent est : « si p est un nombre premier et si a est un entier quelconque, alors a p – a est un multiple de p » : Il doit son nom à Pierre de Fermat, qui l'énonce pour la première fois en 1640. Il dispose de nombreuses applications, à la fois en arithmétique modulaire et en cryptographie. Leonhard Euler présente en 1736 la première démonstration publiée du théorème. Nombre de Carmichael (Page Wikipedia) En théorie des nombres, un nombre de Carmichael (nommé d'après le mathématicien américain Robert Daniel Carmichael), ou nombre absolument pseudo-premier, est un nombre composé n qui vérifie la propriété suivante : pour tout entier a premier avec n, n est un diviseur de an – a ou, ce qui (d'après le lemme de Gauss) est équivalent : pour tout entier a premier avec n, n est un diviseur de an – 1 – 1.
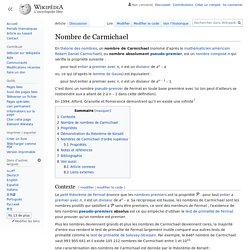
C'est donc un nombre pseudo-premier de Fermat en toute base première avec lui (on peut d'ailleurs se restreindre aux a allant de 2 à n – 1 dans cette définition). En 1994, Alford, Granville et Pomerance démontrent qu'il en existe une infinité[1]. Programme en python donnant les premiers nombres de Carmichael. 5 juin - Substitution polyalphabétique - A lire. 5 juin - Décoder la phrase (Feuille de calcul à télécharger) 5 juin - Codage affine décodage (Feuille de calcul à télécharger) Enigma (Page wikipedia) Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes »(janvier 2015).
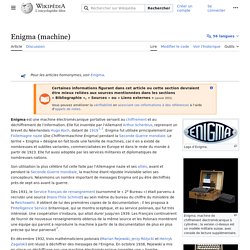
Améliorez sa vérifiabilité en les associant par des références à l'aide d'appels de notes. Enigma, une machine de chiffrement électromécanique à cylindres ; la version ci-dessus est un modèle militaire suisse, avec une console de lecture supplémentaire. Enigma est une machine électromécanique portable servant au chiffrement et au déchiffrement de l'information. Elle fut inventée par l'Allemand Arthur Scherbius, reprenant un brevet du Néerlandais Hugo Koch, datant de 1919[1],[2]. Enigma fut utilisée principalement par les Allemands (Die Chiffriermaschine Enigma) pendant la Seconde Guerre mondiale. Son utilisation la plus célèbre fut celle faite par l'Allemagne nazie et ses alliés, avant et pendant la Seconde Guerre mondiale, la machine étant réputée inviolable selon ses concepteurs. Et. 5 juin - Vigenère (Feuille de calcul à télécharger) 29 mai - Le chiffrement affine - A lire. 29 mai - Le chiffrement affine - Feuille de calcul. Étienne Bézout. Un article de Wikipédia, l'encyclopédie libre.
Biographie[modifier | modifier le code] Publications[modifier | modifier le code] Cours de mathématiques à l'usage des gardes du pavillon et de la marine, première partie Éléments d'arithmétique, Imprimerie Ph. -D. Pierres, Paris, 1781 (lire en ligne) [archive]Cours de mathématiques à l'usage des gardes du pavillon et de la marine, seconde partie contenant les éléments de géométrie, la trigonométrie rectiligne & la trigonométrie sphérique, Imprimerie Ph. Mémoires de l'Académie royale des sciences[modifier | modifier le code] Mémoires de mathématique et de physique présentés à l'Académie royale des sciences[modifier | modifier le code] Mémoire sur les quantités différencielles, qui n'étant point intégrables par elles-mêmes, le deviennent néanmoins quand on leur joint des quantités de même forme qu'elles, Imprimerie royale, Paris, 1760, tome 3, p. 326-343 (lire en ligne) [archive]
Carl Friedrich Gauss. Signature La qualité extraordinaire de ses travaux scientifiques était déjà reconnue par ses contemporains.
Dès 1856, le roi de Hanovre fit graver des pièces commémoratives avec l'image de Gauss et l'inscription Mathematicorum Principi (« au prince des mathématiciens » en latin). Gauss n'ayant publié qu'une partie de ses découvertes, la postérité découvrit surtout l'étendue de ses travaux lors de la publication de ses Œuvres, de son journal et d'une partie de ses archives, à la fin du xixe siècle.
Gauss dirigea l'Observatoire de Göttingen et ne travailla pas comme professeur de mathématiques — d'ailleurs il n'aimait guère enseigner — mais il encouragea plusieurs de ses étudiants, qui devinrent d'importants mathématiciens, notamment Gotthold Eisenstein et Bernhard Riemann. Biographie[modifier | modifier le code] Il commence sa scolarité en 1784 à la Katharinen Volksschule, une petite école élémentaire proche de son domicile ; le professeur J.G. 20200424 Activités sur le théorème de Gauss. 20200424 Activités sur le théorème de Gauss Correction.
20200424 Equations ax by. 15 mai - Equations diophantiennes. 15 mai - QCM Sujet.