Les polynomes. Polynôme. Un polynôme, en algèbre générale, à une indéterminée sur un anneau unitaire est une expression de la forme : où X est un symbole appelé indéterminée du polynôme, supposé être distinct de tout élément de l'anneau, les coefficients ai sont dans l'anneau, et n est un entier naturel.
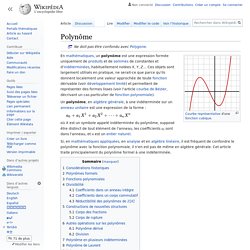
Considérations historiques[modifier | modifier le code] L'histoire des polynômes est inséparable de celle de l'algèbre. Initialement créés pour résoudre des équations, ils se trouvent confondus avec les fonctions polynomiales. Au fur et à mesure que les recherches s'approfondissent, il se révèle nécessaire de distinguer plus nettement le polynôme formel de la fonction polynomiale. Polynômes formels[modifier | modifier le code] Un polynôme f à une indéterminée est défini comme une expression formelle de la forme où les coefficients a0, .., an sont éléments d'un anneau A, et X est un symbole formel appelé indéterminée du polynôme. , c'est le plus grand exposant de X devant lequel le coefficient n'est pas nul. Degré d'un polynôme. Par exemple, le polynôme 7X2Y3 + 4X – 9 a trois monômes.
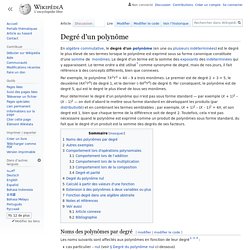
Le premier est de degré 2 + 3 = 5, le deuxième (4X1Y0) de degré 1, et le dernier (–9X0Y0) de degré 0. Par conséquent, le polynôme est de degré 5, qui est le degré le plus élevé de tous ses monômes. Coefficients et degrés des termes d'un polynôme. Polynôme du second degré : définition - coefficients - pièges à éviter - Première S - ES -STI. Polynôme du second degré : Les 3 techniques pour écrire sous forme canonique - Première S ES STI. Équations du Second degré et sup.
Polynômes et fractions rationnelles. GRANDS CLASSIQUES DE CONCOURS : POLYNOMES. PolynomesBernstein. Méthodes de quadrature de Gauss. Les formules de Gauss jouent un rôle fondamental dans la méthode des éléments finis.
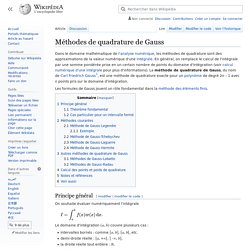
Principe général[modifier | modifier le code] On souhaite évaluer numériquement l'intégrale Le domaine d'intégration (a, b) couvre plusieurs cas : intervalles bornés : comme [a, b], [a, b[, etc.demi-droite réelle : [a, +∞[, ] -∞, b],la droite réelle tout entière : ℝ. [UT#26] Construction des polynômes interpolateurs de Lagrange. Formule du polynôme de Lagrange. [UT#27] Autour du phénomène de Runge. Polynômes de Legendre. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Ce sont les polynômes, notés ici Pn , de degré n, vérifiant Pn(1) = 1 et définis sur l'intervalle [-1,1] orthogonaux pour le produit scalaire (cf. exercice 1) de densité Φ = 1 : Ces polynômes, issus de travaux de Legendre en théorie du potentiel se rencontrent dans la recherche des solutions de l'équation de Laplace, dites fonctions harmoniques.
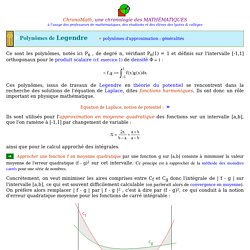
Ils ont donc un rôle important en physique mathématique. Équation de Laplace, notion de potentiel : » Ils sont utilisés pour l'approximation en moyenne quadratique des fonctions sur un intervalle [a,b], que l'on ramène à [-1,1] par changement de variable : ainsi que pour le calcul approché des intégrales. ➔ Approcher une fonction f en moyenne quadratique par une fonction g sur [a,b] consiste à minimiser la valeur moyenne de l'erreur quadratique (f - g)2 sur cet intervalle. Courbes de Bézier. Polynôme de Tchebychev. En mathématiques, un polynôme de Tchebychev est un terme de l'une des deux suites de polynômes orthogonaux particulières reliées à la formule de Moivre.
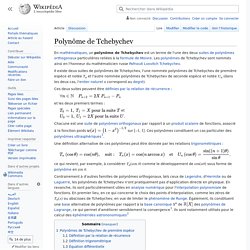
Les polynômes de Tchebychev sont nommés ainsi en l'honneur du mathématicien russe Pafnouti Lvovitch Tchebychev. Il existe deux suites de polynômes de Tchebychev, l'une nommée polynômes de Tchebychev de première espèce et notée Tn et l'autre nommée polynômes de Tchebychev de seconde espèce et notée Un (dans les deux cas, l'entier naturel n correspond au degré). Ces deux suites peuvent être définies par la relation de récurrence : et les deux premiers termes : et sur [–1, 1]. Une définition alternative de ces polynômes peut être donnée par les relations trigonométriques : ce qui revient, par exemple, à considérer Tn(cos θ) comme le développement de cos(nθ) sous forme de polynôme en cos θ. Spline (mathematics) Single knots at 1/3 and 2/3 establish a spline of three cubic polynomials meeting with C2 continuity.
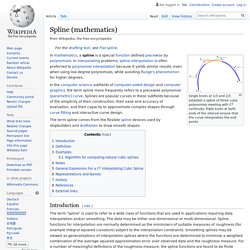
Triple knots at both ends of the interval ensure that the curve interpolates the end points In the computer science subfields of computer-aided design and computer graphics, the term spline more frequently refers to a piecewise polynomial (parametric) curve. Splines are popular curves in these subfields because of the simplicity of their construction, their ease and accuracy of evaluation, and their capacity to approximate complex shapes through curve fitting and interactive curve design. The term spline comes from the flexible spline devices used by shipbuilders and draftsmen to draw smooth shapes.
The term "spline" is used to refer to a wide class of functions that are used in applications requiring data interpolation and/or smoothing. We begin by limiting our discussion to the univariate polynomial case. Spline Command - GeoGebra Manual. From GeoGebra Manual.