

Biographie de Paul Painlevé. Paul Painlevé fut un grand mathématicien au tournant du XIXè et du XXè siècle, peut-être pas le plus grand, mais probablement un des plus connus hors du sérail scientifique, tant il eut en effet une carrière politique brillante qui l'amena à exercer les plus hautes responsabilités au sommet de l'état.

Fils d'un dessinateur lithographe, il effectue des études brillantes dans les "grands lycées" parisiens, avant d'intégrer l'Ecole Normale Supérieure en 1883. Painlevé Paul. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Entré à L'École normale supérieure en 1883, agrégé de mathématiques session 1886, Paul Painlevé est docteur ès sciences un an plus tard, sa thèse, Sur les lignes singulières des fonctions analytiques, était dirigée par Picard.

MetriquePainleve. Mathématiciens et entreprise, une longue histoire - WebTV Université de Lille. Pappus d'Alexandrie. Pappus d'Alexandrie — nom latinisé de Pappos d'Alexandrie, en grec Πάππος ὁ Ἀλεξανδρεύς — est l'un des plus importants mathématiciens de la Grèce antique.
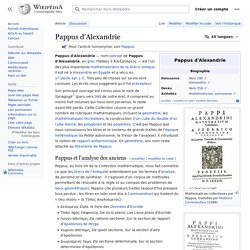
Il est né à Alexandrie en Égypte et a vécu au IVe siècle apr. J. -C. Très peu de choses sur sa vie sont connues. Les écrits nous suggèrent qu'il fut précepteur. Son principal ouvrage est connu sous le nom de Synagogè[1] (paru vers 340 de notre ère). Pappus. On ne sait quasiment rien de la vie de Pappus.

Un texte du Xème siècle (la Souda, une encyclopédie grecque) dit que « le philosophe Pappus d'Alexandrie vécut environ à l'époque de l'empereur Theodosius Ier, au moment où Theon, auteur du Canon de Ptolémée, prospérait », ce qui nous place dans la seconde moitié du IVème siècle. Cependant une autre chronologie, due justement à Theon, situe Pappus un siècle plus tôt. La seconde hypothèse fut souvent privilégiée, mais il semble aujourd'hui qu'aucune des deux sources ne soit bonne ! La meilleure estimation est due à une éclipse citée par Pappus. Or une éclipse a bien eu lieu à Alexandrie le 18 octobre 320. Source :Université St-Andrews. Figures du problème de Pappus.
La Géométrie - Problème de Pappus - Page 304 Haut de cette page et pages précédentes, voir la première partie du livre premier Exemple tiré de Pappus Et on peut le voir aussi fort clairement de ce que Pappus a mis au commencement de son septième livre, où après s'être arrêté quelque temps à dénombrer tout ce qui avait été écrit en géométrie par ceux qui l'avaient précédé, il parle enfin d'une question qu'il dit que ni Euclide, ni Apollonius, ni aucun autre, n'avaient su entièrement résoudre ; et voici ses mots : Je cite plutôt la version latine que le texte grec, afin que chacun l'entende plus aisément Mais ce lieu à 3 et 4 lignes, dont Apollonius dit, à propos de son livre III, qu'Euclide ne l'a pas complètement traité, lui-même, pas plus qu'aucun autre, n'aurait pu l'achever, ni même rien ajouter à ce qu'Euclide en a écrit, du moins en s'en tenant exclusivement aux Éléments des Coniques déjà démontrés au temps d'Euclide, etc.

Principe de Pareto. Un article de Wikipédia, l'encyclopédie libre.
Pour les articles homonymes, voir Pareto. Le principe de Pareto, aussi appelé loi de Pareto, principe des 80-20 ou encore loi des 80-20, est un phénomène empirique constaté dans certains domaines : environ 80 % des effets sont le produit de 20 % des causes. Il a été appliqué à des domaines comme le contrôle qualité. On considère souvent que les phénomènes pour lesquels ce principe est vérifié suivent une forme particulière de distribution de Pareto.
Naissance du principe[modifier | modifier le code] Loi de Pareto. Un article de Wikipédia, l'encyclopédie libre.
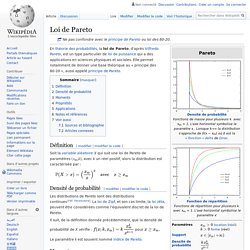
En théorie des probabilités, la loi de Pareto, d'après Vilfredo Pareto, est un type particulier de loi de puissance qui a des applications en sciences physiques et sociales. Elle permet notamment de donner une base théorique au « principe des 80-20 », aussi appelé principe de Pareto. Définition[modifier | modifier le code] Soit la variable aléatoire X qui suit une loi de Pareto de paramètres (xm,k), avec k un réel positif, alors la distribution est caractérisée par : Densité de probabilité[modifier | modifier le code] Les distributions de Pareto sont des distributions continues[réf. nécessaire]. Marc-Antoine Parseval des Chênes. Marc-Antoine Parseval des Chênes Marc-Antoine Parseval des Chênes, né le 27 avril 1755 à Rosières-aux-Salines[1] et mort le 16 août 1836 à Paris, est un mathématicien français.
On a donné son nom à l'égalité de Parseval, une formule fondamentale de la théorie des séries de Fourier. Biographie[modifier | modifier le code] Jeunesse, poésie et politique[modifier | modifier le code] Le théorème de Parseval. Théorème de Parseval. [UT#35] Égalité de Parseval et calcul de ζ(2) Blaise Pascal. Blaise Pascal était un mathématicien, physicien, philosophe et théologien français né en 1623 à Clermont-Ferrand en Auvergne et mort à Paris en 1662.

BNF ESSENTIELS. Blaise Pascal - Physicien, mathématicien, philosophe et théologien. Blaise Pascal (1623-1662) était un physicien, mathématicien, philosophe et théologien français.
Auteur de la célèbre phrase : « Le cœur a ses raisons, que la raison ne connaît point ». Blaise Pascal est né à Clermont-Ferrand, le 19 juin 1623. Aspects esthétiques du Traité du Triangle arithmétique. Blaise Pascal. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Philosophe de renom, auteur des célèbres Pensées, mathématicien et physicien. Sa mère mourut alors qu'il n'avait que 3ans; il fut élevé et instruit par son père Étienne Pascal, comptable et mathématicien reconnu (1588-1651) de l'époque (celle de Mersenne), à qui l'on doit l'étude du limaçon portant son nom, en fait une conchoïde de cercle.
. | Le théorème de Pascal. Théorème sur la colinéarité de trois points générés à partir d'un hexagone inscrit sur une conique Ligne Pascal GHK de l'hexagone auto-croisé ABCDEF inscrit dans l'ellipse. Les côtés opposés de l'hexagone ont la même couleur. Les intersections des côtés opposés étendus de l' hexagone cyclique simple ABCDEF (à droite) se trouvent sur la droite de Pascal MNP (à gauche). A 16 Year Old Discovered This AMAZING Geometry Hidden Pattern. Pascal's Theorem. Émission cogito: Pascal. Cp blaise pascal. Soulé Christophe - "Le triangle de Pascal et ses propriétés" - 2008. On sait bien que Blaise Pascal fut un mathématicien et un physicien génial avant de se consacrer à la théologie et la philosophie. Parmi ses travaux mathématiques figure l'important Traité du triangle arithmétique de 1654. Même si le tableau de nombres entiers qui y est défini avait déjà été étudié plusieurs siècles auparavant par Yang Hui et Omar Khayyam, c'est bien sous le nom de «triangle de Pascal» qu'il est connu jusqu'à nos jours.
Les nombres apparaissant dans le triangle de Pascal (appelés coefficients binomiaux) sont utiles dans de nombreuses situations, depuis les identités remarquables de l'algèbre jusqu'à des problèmes combinatoires complexes, en passant par le calcul des chances de gagner au Loto. L'arithmétique (ou théorie des nombres) est la branche des mathématiques qui s'intéresse aux propriétés des nombres entiers, notamment aux questions de divisibilité et aux nombres premiers (ceux qui ne sont divisibles que par 1 et eux-mêmes). Le cycle "Un texte, un mathématicien" L'étonnant triangle de Pascal ! Pascal la Géométrie du hasard. D. Perrin - Le théorème de Pascal. Pascal, Roberval et la quadrature de la cycloïde (Thierry Lambre) [CM#1] La Machine Arithmétique de Pascal. D. Perrin - Le théorème de Pascal - PeerTube. Triangle de Pascal et coefficients binomiaux. Biographie de Pappus.
Pappus est le dernier des grands mathématiciens grecs. On sait très peu de choses de sa vie, et les chronologies qui y font référence sont contradictoires! De ses écrits, on peut juste extraire qu'il est né et a sans doute vécu à Alexandrie, qu'il y enseigna, qu'il eut un fils, Hermodorus, et qu'il assista à une éclipse du soleil qu'on a pu dater au 18 octobre 320.
Son travail majeur est Synagoge, traduit en français sous le nom de Collection Mathématique. Dans cet ouvrage en 8 tomes, dont une partie est perdue, Pappus reprend les travaux des grands géomètres grecs (dont Euclide, Ptolémée, Archimède), il améliore parfois leurs démonstrations ou complète leurs résultats. Pappus d'Alexandrie. George Peacock. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Fils de Pasteur, instruit par son père, George Peacock entame des études supérieures à Richmond, qu'il poursuivit au Trinity College de Cambridge (1809) où il rencontra Babbage qui devint son ami. Assistant puis professeur (1837) de géométrie et d'astronomie en ce collège réputé d'Angleterre, Peacock tentera d'imposer, s'opposant aux fluxions de Newton, les idées du calcul différentiel selon Leibniz en promouvant avec son ami, et le déjà renommé astronome John Herschel, le traité de Lacroix sur ce vaste et fondamental sujet.
Les trois jeunes scientifiques créèrent alors (1815) l'Analytical Society. i John Frederick William Herschel (1792-1871) est le fils de Friedrich Wilhelm Herschel (1738-1822), d'origine allemande, astronome à qui l'on doit en particulier la découverte d'Uranus en 1781. . ➔ Pour en savoir plus : Möbius. Biographie de Giuseppe Peano. Giuseppe Peano est un mathématicien et philosophe italien dont les travaux les plus importants datent de la fin du XIXè siècle. Peano : les axiomes de N. Giuseppe Peano naît le 27 août 1858 à Cuneo. Peano Giuseppe. Pearson Karl. Peirce Charles Sanders. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges.
Walter Francis Penney. Walter Francis Penney ou Walter Penney (18 janvier 1913 à New York - 24 juin 2000 à Greenbelt (Maryland)) est un mathématicien américain[1],[2],[3]. Il était spécialisé en cryptanalyse et avait fait carrière dans la Crypto Analysis Group de la US Navy, devenue plus tard la NSA[1],[3]. Le paradoxe de Penny. Le paradoxe de Penney a été formulé en 1969 par Walter H. Roger Penrose. Roger Penrose en 2005. Roger Penrose — Wikipédia.
English mathematical physicist Sir Roger Penrose Kt OM FRS (born 8 August 1931) is a British mathematician, mathematical physicist, philosopher of science and Nobel Laureate in Physics.[1] He is Emeritus Rouse Ball Professor of Mathematics at the University of Oxford, an emeritus fellow of Wadham College, Oxford, and an honorary fellow of St John's College, Cambridge, and University College London.[2] Penrose has made contributions to the mathematical physics of general relativity and cosmology. Penrose. Pavages de Penrose. Roger Penrose - Is Mathematics Invented or Discovered? La légende Grigori Perelman. SYNOPSIS D’UNE AVENTURE FABULEUSE. Scoop : il refuse un prix de un millions de dollars ! Deux (deux?) minutes pour la conjecture de Poincaré devenue théorème de Perelman. Problems in Topology, Post-Perelman - Stephen Smale. Perelman refuse la Medaille Fields.
Géométriser l'espace : de Gauss à Perelman. Rozsa Péter. Rózsa Péter. Michel Pétrovitch. Michel Pétrovitch. Michel Petrovitch Sur une fonctionnelle. Un problème sur la chaleur rayonnant par Michel Petrovitch. Del Pezzo Surfaces. Émile Picard. DEUX OU TROIS CHOSES QUE JE SAIS D’ÉMILE PICARD... Georg Pick. Théorème de Pick. Pincherle Salvatore. Joseph Plateau. John Playfair. L'axiome de Playfair. Leo Pochhammer. Symbole de Pochhammer. Polynômes de Pochhammer. Karl Wilhelm Pohlke.
Louis Poinsot. UNE GÉOMÉTRIE DE L’ORDRE ET DE LA SITUATION AU XIXE SIÈCLE. POLYGONES ET THÉORIE DES NOMBRES CHEZ LOUIS POINSOT. Biographie de Siméon Denis Poisson. Poisson : les mathématiques par erreur. Siméon Denis Poisson. Siméon Denis Poisson. Simeon Denis Poisson. George Polya. Les leçons de Polya: Comment découvrir une démonstration pourtant longue et complexe. T. Gowers - Comment découvrir une démonstration pourtant longue et complexe : les leçons de Polya. Jean-Victor Poncelet. Poncelet, réinventeur de la géométrie projective. Biographie de Jean-Victor Poncelet, géomètre. Poncelet Jean Victor. Théorème de Poncelet-Steiner. Grand théorème de Poncelet. Porisme de Poncelet et coniques de saut. Une nouvelle preuve du porisme de Poncelet. À propos des variétés de Poncelet. Biographie de Claude Ptolémée. Claude Ptolémée (IIe siècle ap. J.-C.) Ptolemee. Almagest. Théorème de Ptolémé. Histoire de Pythagore. Mathématiques - Petite biographie de Pythagore.
Biographie et principaux travaux du mathématicien Pythagore. Pythagore : l'histoire d'un théorème.