

Probabilidad Estadística. Distribución Uniforme. Estudiantes Ingeniería Civil UNEFA Caracas. MEDIA Y LA VARIANZA DE LAS DISTRIBUCIONES DISCRETAS VIDEOS. Introducción a las distribuciones de probabilidad discretas. Una distribución de probabilidad es una representación de todos los resultados posibles de algún experimento y de la probabilidad relacionada con cada uno. Una distribución de probabilidad es discreta cuando los resultados posibles del experimento son obtenidos de variables aleatorias discretas, es decir, de variables que sólo puede tomar ciertos valores , con frecuencia números enteros, y que resultan principalmente del proceso de conteo.
Ejemplos de variables aleatorias discretas son: Número de caras al lanzar una moneda El resultado del lanzamiento de un dado Número de hijos de una familia Número de estudiantes de una universidad Ejemplo ilustrativo: Sea el experimento aleatorio de lanzar 2 monedas al aire . El espacio muestral es S = {CC, CS, SC, SS} La probabilidad de cada punto muestral es de 1/4, es decir, P(CC) = P(CS) = P(SC) = P(SS) = 1/4 La distribución de probabilidades del número de caras se presenta en la siguiente tabla: Interpretación: Donde: = Posible resultado Ejemplo ilustrativo: AREA DE DISTRIBUCION NORMAL. VARIANZA NORMAL. AREA DE DISTRIBUCION NORMAL. TABLA POISSON. Tabla x. DISTRIBUCIÓN DE PROBABILIDADES. La distribución Binomial es un caso particular de probabilidad de variable aleatoria discreta, y por sus aplicaciones, es posiblemente la más importante.
Esta distribución corresponde a la realización de un experimento aleatorio que cumple con las siguientes condiciones: * Al realizar el experimento sólo son posible dos resultados: el suceso A, llamado éxito, y el suceso B , llamado fracaso. * Al repetir el experimento, el resultado obtenido es independiente de los resultados obtenidos anteriormente. * La probabilidad del suceso A es constante, es decir, no varía de una prueba del experimento a otra. * En cada experimento se realizan n pruebas idénticas. Todo experimento que tenga estas características se dice que sigue el modelo de la distribución Binomial o distribución de Bernoulli.
Probabilidad Tablas de contingencia Matematicas 2º Bachillerato AINTE. Digitalización de bienvenida. Teorema de Bayes. En la teoría de la probabilidad el teorema de Bayes es un resultado enunciado por Thomas Bayes en 1763[1] que expresa la probabilidad condicional de un evento aleatorio A dado B en términos de la distribución de probabilidad condicional del evento B dado A y la distribución de probabilidad marginal de sólo A.
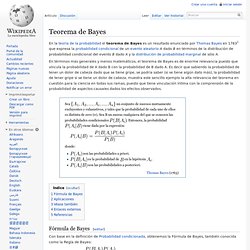
En términos más generales y menos matemáticos, el teorema de Bayes es de enorme relevancia puesto que vincula la probabilidad de A dado B con la probabilidad de B dado A. Es decir que sabiendo la probabilidad de tener un dolor de cabeza dado que se tiene gripe, se podría saber (si se tiene algún dato más), la probabilidad de tener gripe si se tiene un dolor de cabeza, muestra este sencillo ejemplo la alta relevancia del teorema en cuestión para la ciencia en todas sus ramas, puesto que tiene vinculación íntima con la comprensión de la probabilidad de aspectos causales dados los efectos observados.
Fórmula de Bayes[editar] Aplicaciones[editar] Como observación, se tiene. PROBABILIDAD TOTAL Y TEOREMA DE BAYES. Teorema de bayes. Ejercicio probabilidad condicional. E) PROBABILIDAD CONDICIONAL. Formula probabilidad condicional. Intro Estadistica Inferencial. 3) DISTRIBUCIÓN HIPERGEOMÉTRICA. Los experimentos que tienen este tipo de distribución tienen las siguientes características: a) Al realizar un experimento con este tipo de distribución, se esperan dos tipos de resultados. b) Las probabilidades asociadas a cada uno de los resultados no son constantes. c) Cada ensayo o repetición del experimento no es independiente de los demás. d) El número de repeticiones del experimento ( n ) es constante.

Ejemplo: En una urna o recipiente hay un total de N objetos, entre los cuales hay una cantidad a de objetos que son defectuosos, si se seleccionan de esta urna n objetos al azar, y sin reemplazo, ¿cuál es la probabilidad de obtener x objetos defectuosos? Solución: Luego; donde: p( x , n ) = probabilidad de obtener x objetos defectuosos de entre n seleccionados muestras de n objetos en donde hay x que son defectuosos y n-x buenos todas las muestras posibles de seleccionar de n objetos tomadas de entre N objetos en total = espacio muestral Solución: N = 10 objetos en total Ejemplos: 4.