

Multi1. 126 5 915. 4 21 polytope - Wikipedia. Its Coxeter symbol is 421, describing its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 4-node sequences, The rectified 421 is constructed by points at the mid-edges of the 421.
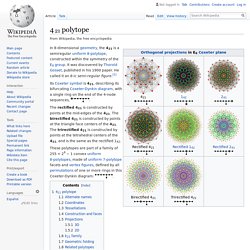
The birectified 421 is constructed by points at the triangle face centers of the 421. The trirectified 421 is constructed by points at the tetrahedral centers of the 421, and is the same as the rectified 142. These polytopes are part of a family of 255 = 28 − 1 convex uniform 8-polytopes, made of uniform 7-polytope facets and vertex figures, defined by all permutations of one or more rings in this Coxeter-Dynkin diagram: 421 polytope[edit] The vertices of this polytope can also be obtained by taking the 240 integral octonions of norm 1. For visualization this 8-dimensional polytope is often displayed in a special skewed orthographic projection direction that fits its 240 vertices within a regular triacontagon (called a Petrie polygon). Alternate names[edit] Coordinates[edit] . . Vertices. About - Project Euler. Digital root. The digital root (also repeated digital sum) of a non-negative integer is the (single digit) value obtained by an iterative process of summing digits, on each iteration using the result from the previous iteration to compute a digit sum.
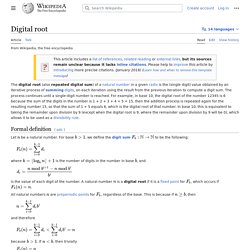
The process continues until a single-digit number is reached. For example, the digital root of 65,536 is 7, because 6 + 5 + 5 + 3 + 6 = 25 and 2 + 5 = 7. Digital roots can be calculated with congruences in modular arithmetic rather than by adding up all the digits, a procedure that can save time in the case of very large numbers. Digital roots can be used as a sort of checksum.
For example, since the digital root of a sum is always equal to the digital root of the sum of the summands' digital roots. Digital roots are used in Western numerology, but certain numbers deemed to have occult significance (such as 11 and 22) are not always completely reduced to a single digit. Logic To Physics. Lorentz force. In physics, particularly electromagnetism, the Lorentz force is the combination of electric and magnetic force on a point charge due to electromagnetic fields.
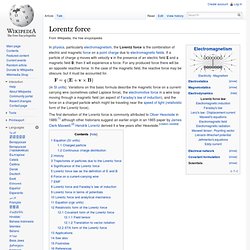
If a particle of charge q moves with velocity v in the presence of an electric field E and a magnetic field B, then it will experience a force. For any produced force there will be an opposite reactive force. In the case of the magnetic field, the reactive force may be obscure, but it must be accounted for. (in SI units). Variations on this basic formula describe the magnetic force on a current-carrying wire (sometimes called Laplace force), the electromotive force in a wire loop moving through a magnetic field (an aspect of Faraday's law of induction), and the force on a charged particle which might be traveling near the speed of light (relativistic form of the Lorentz force).
Equation (SI units)[edit] Charged particle[edit] Phonon. Phonons play a major role in many of the physical properties of condensed matter, such as thermal conductivity and electrical conductivity.
The study of phonons is an important part of condensed matter physics. The concept of phonons was introduced in 1932 by Russian physicist Igor Tamm. The name phonon comes from the Greek word φωνή (phonē), which translates as sound or voice because long-wavelength phonons give rise to sound. Shorter-wavelength higher-frequency phonons give rise to heat. Diamagnetism. Diamagnets were first discovered when Sebald Justinus Brugmans observed in 1778 that bismuth and antimony were repelled by magnetic fields.
The term diamagnetism was coined by Michael Faraday in September 1845, when he realized that every material responded (in either a diamagnetic or paramagnetic way) to an applied magnetic field. [citation needed] Materials[edit] Diamagnetic materials, like water, or water based materials, have a relative magnetic permeability that is less than or equal to 1, and therefore a magnetic susceptibility less than or equal to 0, since susceptibility is defined as χv = μv − 1. This means that diamagnetic materials are repelled by magnetic fields.
All conductors exhibit an effective diamagnetism when they experience a changing magnetic field. Superconductors[edit] Transition from ordinary conductivity (left) to superconductivity (right). Demonstrations[edit] Curving water surfaces[edit] Levitation[edit] Theory[edit] Langevin diamagnetism[edit] , where . I Ching Genetic Code HyperDiamond Physics. Vienna Center for Quantum Science and Technology: Start. What is Chaos? An Interactive Online Course for Everyone.