

Monad Transformers. Arrows. The Task abstraction. Neil Mitchell, Simon Peyton Jones and I have just finished a paper describing a systematic and executable framework for developing and comparing build systems.

The paper and associated code are available here: The code is not yet well documented and polished, but I’ll bring it in a good shape in April. You can learn more about the motivation behind the project here. In this blog post I would like to share one interesting abstraction that we came up with to describe build tasks: type Task c k v = forall f. c f => (k -> f v) -> k -> Maybe (f v) A Task is completely isolated from the world of compilers, file systems, dependency graphs, caches, and all other complexities of real build systems.
This highly-abstracted type is best introduced by an example. Here cell A1 contains the value 10, cell B1 contains the formula A1 + A2, etc. Functors, Applicatives, And Monads In Pictures - adit.io. Updated: May 20, 2013 Here's a simple value: And we know how to apply a function to this value: Simple enough.
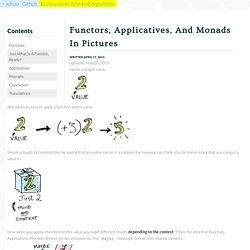
Lets extend this by saying that any value can be in a context. For now you can think of a context as a box that you can put a value in: Now when you apply a function to this value, you'll get different results depending on the context.
Haskell Matrices. A Monad in Practicality: Controlling Time - Soreλ\a's Basement. Concurrency is quite a big deal, specially these days where everything must be “web scale.”

There are several models of concurrency, each with their own pros and cons, in this article I present a composable alternative to the widespread non-blocking model of concurrency, which generally uses Continuation-Passing style where each computation accepts a “continuation” or “callback,” instead of returning the result of the computation to the caller. In a language where some computations return a value to the caller and some take a continuation as an argument, we can’t really apply our well-established and general compositional operators, such as function composition, because the rules they rely on have been broken. This is why things may quickly descend into callback-hell and spaghetti of callsite-specific functionality — we lose all of the organisational patterns we are used to.
Note: Previous knowledge of monads or category theory are not necessary to read this blog post. 1. 2. 2.1. 2.2. Typeclassopedia. By Brent Yorgey, byorgey@cis.upenn.edu Originally published 12 March 2009 in issue 13 of the Monad.Reader.
Ported to the Haskell wiki in November 2011 by Geheimdienst. This is now the official version of the Typeclassopedia and supersedes the version published in the Monad.Reader. Please help update and extend it by editing it yourself or by leaving comments, suggestions, and questions on the talk page. The standard Haskell libraries feature a number of type classes with algebraic or category-theoretic underpinnings. The goal of this document is to serve as a starting point for the student of Haskell wishing to gain a firm grasp of its standard type classes.
Have you ever had any of the following thoughts? What the heck is a monoid, and how is it different from a monad? If you have, look no further! There are two keys to an expert Haskell hacker’s wisdom: Understand the types. The second key—gaining deep intuition, backed by examples—is also important, but much more difficult to attain. Merging, Folding, Monoids, and Foldable. I recently had need to merge a collection of sorted lists.
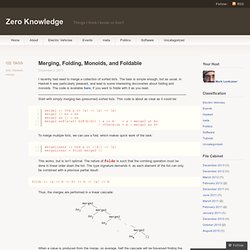
The task is simple enough, but as usual, in Haskell it was particularly pleasant, and lead to some interesting discoveries about folding and monoids. The code is available here, if you want to fiddle with it as you read. Start with simply merging two (presumed) sorted lists. This code is about as clear as it could be: To merge multiple lists, we can use a fold, which makes quick work of the task: This works, but is isn’t optimal. Thus, the merges are performed in a linear cascade: When a value is produced from the merge, on average, half the cascade will be traversed finding the next value. Because merge2 is an associative operation, the merges could instead be arranged in a tree: The number of applications of merge2 is about the same: n−1 vs. n. Let’s create this kind of fold:
The Implementation of Functional Programming Languages. Patterns in Functional Programming. Prompted by some recent work I’ve been doing on reasoning about monadic computations, I’ve been looking back at the work from the 1990s by Phil Trinder, Limsoon Wong, Leonidas Fegaras, Torsten Grust, and others, on monad comprehensions as a framework for database queries.

The idea goes back to the adjunction between extension and intension in set theory—you can define a set by its extension, that is by listing its elements: or by its intension, that is by characterizing those elements: Expressions in the latter form are called set comprehensions. They inspired a programming notation in the SETL language from NYU, and have become widely known through list comprehensions in languages like Haskell. The structure needed of sets or of lists to make this work is roughly that of a monad, and Phil Wadler showed how to generalize comprehensions to arbitrary monads, which led to the “do” notation in Haskell. List comprehensions as is drawn from and from and such that. Typeclassopedia.
Parallelism. Generics. FRP. Monads. Monoids.