

Adjacency matrix. The relationship between a graph and the eigenvalues and eigenvectors of its adjacency matrix is studied in spectral graph theory.
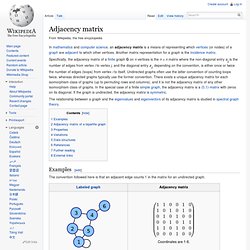
Examples[edit] The convention followed here is that an adjacent edge counts 1 in the matrix for an undirected graph. The adjacency matrix of a complete graph contains all ones except along the diagonal where there are only zeros.The adjacency matrix of an empty graph is a zero matrix. Adjacency matrix of a bipartite graph[edit] The adjacency matrix of a bipartite graph whose parts have and vertices has the form where is an matrix, and represents the zero matrix.
Uniquely represents the bipartite graphs. Be a bipartite graph with parts . 0-1 matrix in which iff If is a bipartite multigraph or weighted graph then the elements are taken to be the number of edges between the vertices or the weight of the edge respectively. Properties[edit] Suppose two directed or undirected graphs with adjacency matrices. Degree (graph theory) A graph with vertices labeled by degree is denoted The maximum degree of a graph G, denoted by Δ(G), and the minimum degree of a graph, denoted by δ(G), are the maximum and minimum degree of its vertices.
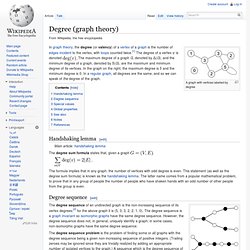
In the graph on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph, all degrees are the same, and so we can speak of the degree of the graph. The degree sum formula states that, given a graph The formula implies that in any graph, the number of vertices with odd degree is even. Two non-isomorphic graphs with the same degree sequence (3, 2, 2, 2, 2, 1, 1, 1). Centrality. Definition and characterization of centrality indices[edit] Next to the following classic centrality indices, there are dozens of other more specialized centrality indices. Despite its intuitive notion there is not yet a definition or characterization of centrality indices which captures all of them.[2] A very loose definition of a centrality index is the following: A centrality index is a real-valued function on the nodes of a graph.
It is a structural index, i.e., if and are two isomorphic graphs and. Weighted network. In a number of real-world networks, not all ties in a network have the same capacity.

In fact, ties are often associated with weights that differentiate them in terms of their strength, intensity, or capacity (Barrat et al., 2004) [2] and Horvath (2011).[3] On the one hand, Mark Granovetter (1973)[4] argued that the strength of social relationships in social networks is a function of their duration, emotional intensity, intimacy, and exchange of services. On the other, for non-social networks, weights often refer to the function performed by ties, e.g., the carbon flow (mg/m²/day) between species in food webs (Luczkowich et al., 2003),[5] the number of synapses and gap junctions in neural networks (Watts and Strogatz, 1998),[6] or the amount of traffic flowing along connections in transportation networks (Opsahl et al., 2008).[7] By recording the strength of ties,[8] a weighted network can be created (also known as a valued network).
Below is an example of such a network: Network science. {{Scienc[1] e}} Network science is an interdisciplinary academic field which studies complex networks such as telecommunication networks, computer networks, biological networks, cognitive and semantic networks, and social networks.
The field draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential modeling from statistics, and social structure from sociology. The United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena. "[2] Background and history[edit] The study of networks has emerged in diverse disciplines as a means of analyzing complex relational data. In the 1930s Jacob Moreno, a psychologist in the Gestalt tradition, arrived in the United States. Department of Defense Initiatives[edit] In 2006, the U.S. Density[edit] .