

Stars. Les solides de Platon. Pourquoi cinq seulement ?

Un polyèdre régulier doit avoir le même nombre de polygones réguliers en chacun de ses sommets. Ce nombre est évidemment au minimum de 3. Le maximum dépendra de l'angle du polygone régulier. En effet si la somme des angles au sommet atteint ou dépasse 360°, nous obtenons un plan ou une superposition des faces. Commençons donc par 3. On peut placer 3 carrés en chaque sommet du polyèdre régulier, nous obtenons le cube. On peut placer 3 pentagones réguliers en chaque sommet du polyèdre régulier, nous obtenons le dodécaèdre.
Platon est né en 427 et mort en 347 avant notre ère. Il est l'un des plus grands philosophes grecs de l'Antiquité, chef d'une Ecole, l'Académie ; ses œuvres sont écrites sous forme de dialogues dont l'un des protagonistes est Socrate, et sa philosophie est l'une des premières philosophies rationalistes. Math'@ctivité 3D : dés solides de Platon. Le résultat final : des dés à jouer en papier.

Ces dés sont des objets en 3 dimensions (3D). Infos... Pourquoi ce nom "Dés solides de Platon" ? : Dans son dialogue de Timée (54c-55d), après avoir décrit les cinq solides, Platon (427-347 av J.C.), philosophe grec, associe les cinq polyèdres réguliers convexes : le tétraèdre régulier, le cube (ou hexaèdre régulier), l'octaèdre régulier, le dodécaèdre régulier et l'icosaèdre régulier, respectivement aux éléments physiques suivants : le feu, la terre, l'air, l'univers et l'eau. II) Les polyèdres réguliers. II) Les polyèdres réguliers 1) Les Solides Platoniciens On connaît depuis l’Antiquité les cinq polyèdres réguliers appelés Solides Platoniciens.

Ces cinq solides peuvent être aisément réalisés à l’aide d’un patron. "A stairway to heaven" Article de François Sauvageot. Double Planetoid. Reptiles. Dimensions - Chapitre 2 - Français. Tomographie. Un article de Wikipédia, l'encyclopédie libre.
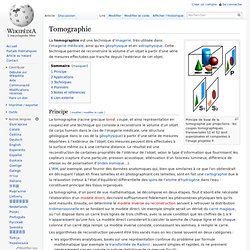
Principe de base de la tomographie par projections : les coupes tomographiques transversales S1 et S2 sont superposées et comparées à l’image projetée P. La tomographie est une technique d’imagerie, très utilisée dans l’imagerie médicale, ainsi qu’en géophysique et en astrophysique. Cette technique permet de reconstruire le volume d’un objet à partir d’une série de mesures effectuées par tranche depuis l’extérieur de cet objet.
Principe[modifier | modifier le code] La tomographie (racine grecque tomê, coupe, et ainsi représentation en coupes) est une technique qui consiste à reconstruire le volume d’un objet (le corps humain dans le cas de l’imagerie médicale, une structure géologique dans le cas de la géophysique) à partir d’une série de mesures déportées à l’extérieur de l’objet. Les algorithmes de reconstruction peuvent être très variés mais on les classe souvent en deux catégories : Applications[modifier | modifier le code] Gravity. File:Universiteit Twente Mesa Plus Escher Object.jpg. Waterfall. Math'@ctivité 3D : casse-tête polyèdre étoilé. Le résultat final est un casse-tête en forme de polyèdre étoilé.

C'est un objet en 3 dimensions (3D). Pour voir le casse-tête en action, cliquer sur l'animation ci-contre puis sur le bouton play. Infos... Un casse-tête polyèdre étoilé ?... : Ce solide, en forme d'étoile en 3D à 12 branches, est un casse-tête tant au niveau de sa construction que de son assemblage. Réalisations en images : Pour voir des réalisations personnelles, en accédant à la rubrique Top10-Images, cliquer sur l'image suivante : .
Atelier p2-20. Dimensions - Chapitre 3 - Français. Math'@ctivité 3D : kaléïdocycle d'ordre 6. Le kaléïdocycle est une Math'@ctivité 3D.

Son patron peut se faire à la main avec des instruments de géométrie traditionnels qui sont ici : la règle graduée, l'équerre et le compas. Il peut aussi se faire à l'aide de l'ordinateur pour le patron en 2D ou pour sa modélisation en 3D avec, entre autres, le logiciel de géométrie dynamique libre 'GeoGebra'. Le résultat final est un anneau de 6, 8 ou 10 tétraèdres (voire plus) selon le cas choisi avec des motifs parfois à la façon d'Escher. Le kaléïdocycle est un objet mathématique et artistique manipulable. Il est un objet en 3 dimensions (3D). Et pour les plus "pressés", ci-après, des figures (motifs) à imprimer (si possible sur des autocollants) pour les coller sur des kaléïdocycles irréguliers d'ordre 6 ou ses coupes par rapport à deux plans de symétrie : , .
Liens Internet : mes incontournables... ..................... Des fichiers d'impression 3D et de découpe automatique ou laser sont disponibles sur mon site à l'adresse : 01p03-kaleidocycle-i6-fiche-enveloppes-apmep-rennes. Editions Kangourou, collèges et lycées. Nouveaux decoupages mathematiques. Decoupages mathematiques. Le cadeau de Kepler. Hypercube - Perspective.